BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Chứng minh gián tiếp trong hình học sơ cấp
- 19/12/2022
- 136 lượt xem
| Đặt vấn đề:
Trong Hình học lớp 9 về tứ giác nội tiếp, khi gặp một bài toán mà yêu cầu của nó giống như một bài toán mà ta đã biết chứng minh, ta có thể sử dụng phương pháp gián tiếp. Để chứng minh gián tiếp ta dựng thêm hình (của một bài toán đã chứng minh) trùng khớp yêu cầu của bài toán cần chứng minh. Sau đó ta chứng minh các sự kiện (đã biết/cần chứng minh) là trùng nhau. |
| Ví dụ 1: Đường thẳng Simson.
Đề thi TS 10 TP HCM năm 2022 |
Lời giải trực tiếp sẽ dựa vào câu a. Ở đây chúng tôi chứng minh gián tiếp dựa vào định lý SimSon.
| Từ một điểm $D$ trên đường tròn ngoại tiếp tam giác $ABC$ ta hạ ba đường vuông góc từ $D$ đến các cạnh $BC, CA, AB$ lần lượt tại $E, F, K$. Khi đó ba điểm $E, F, K$ thẳng hàng trên đường thẳng mà ta gọi là đường thẳng Simson. |
Phép chứng minh sau đây vừa là chứng minh định lý Simson vừa là chứng minh bài thi TS 10 năm 2022 của TP HCM.
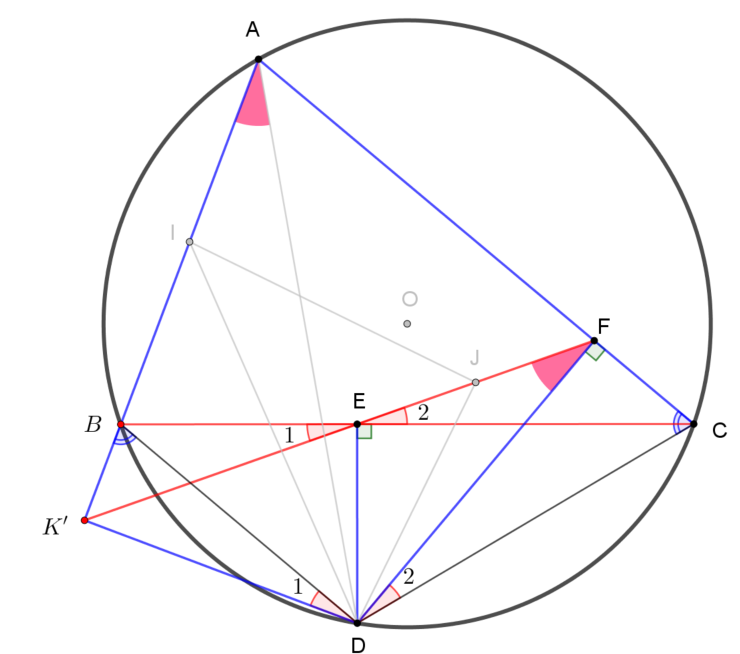
Hạ $BK’\perp AB$. Ta chứng minh $K’, E, F$ thẳng hàng.
| Đây là chứng minh định lý Simson. Suy ra $K’\in EF$, do đó $K’\equiv K$. |
Ta có: Tứ giác $DEFC$ nội tiếp đường tròn đường kính $DC$.
$\widehat{E_2}=\widehat{D_2}$ (cùng chắn cung $FC$) $=90^\circ – \widehat{ACD}$.
Hoàn toàn tương tự
$\widehat{E_1}=\widehat{D_1}$ (cùng chắn cung $BK’$) $=90^\circ – \widehat{DBK’}$.
Mà $\widehat{ACD}=\widehat{DBK’}$ (tứ giác $ABDC$) nội tiếp).
Vậy $\widehat{E_1}=\widehat{E_2}$ nên 3 điểm $K’, E, F$ thẳng hàng.
Suy ra $K’$ là giao điểm của đường thẳng $EF$ và $AB$ nên $K’\equiv K$.
Tứ giác $BKDE$ có $\widehat{BKB}+\widehat{BED}=90^\circ+90^\circ=180^\circ$ nên là tứ giác nội tiếp.
| Ví dụ 2: Tam giác $ABC$ nhọn $AB<AC$. Gọi $H$ là trực tâm của tam giác. Vẽ đường tròn $(O)$ đường kính $BC$. Từ $H$ hạ đường vuông góc với $AO$ tại $I$. Tia $HI$ cắt $(O)$ tại $N$. Chứng minh $AN$ là tiếp tuyến của đường tròn. |
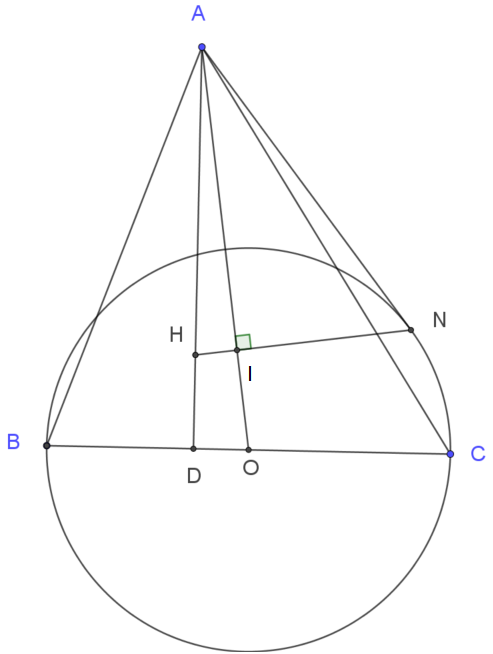
Để chứng minh $AN$ là tiếp tuyến của $(O)$ (theo ycbt) từ $A$ ta vẽ hai tiếp tuyến $AM, AN’$ tới $(O)$ sao cho tiếp điểm $N’$ nằm trên cung nhỏ được chắn bởi hai tia $OC$ và $OA$. Ta chứng minh $M, H, N’$ thẳng hàng.
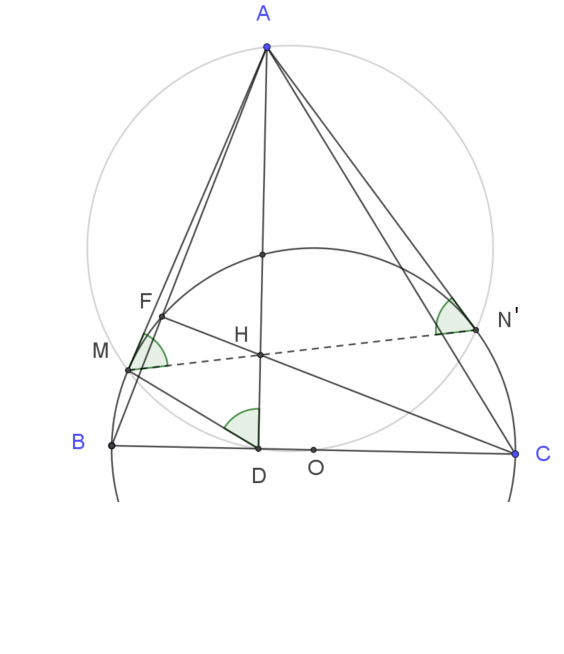
| Khi đó $AO$ sẽ cắt đường thẳng $MHN’$ tại điểm $I’\equiv I$ (vì cùng là hình chiếu vuông góc của $H$ trên $AO$). Khi đó $N’$ là giao của tia $HI$ với $(O)$ nên $N’\equiv N$, nghĩa là $AN$ là tiếp tuyến của $(O)$. |
Trong đường tròn $(O)$ ta có $AM^2=AF.AB$ ($F$ là chân đường cao từ $C$).
Tứ giác $HFBD$ nọi tiếp đường tròn đường kính $BH$ nên $AF.AB=AH.AD$.
Vậy $AM^2=AH.AD$. Suy ra $\triangle AMH \backsim \triangle ADM$. Suy ra $\widehat{AMH}=\widehat{ADM}$.
Trong đường tròn đường kính $AO$ các góc $\widehat{ADM}$ và $\widehat{AMN’}$ cùng chắn cung $AM$ nên $\widehat{ADM} = \widehat{AN’M}$, mà $\widehat{AN’M}=\widehat{AMN’}$.
Tóm lại $\widehat{AMH}=\widehat{AMN’}$. Vậy $M, H, N’$ thẳng hàng.
About TS. Nguyễn Thái Sơn
