BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
fx-570VN PLUS Giải câu cực trị số phức trong ĐMH mà không cần vẽ hình
- 06/04/2018
- 1,325 lượt xem
Sử dụng tính năng SOLVE nhằm phỏng đoán và giải bài toán cực trị của số phức mà không thông qua vẽ hình
Có một bạn học sinh đã gửi tới Diễn đàn bài toán sau (Trích trong đề thi minh họa của Bộ Giáo dục và đào tạo lần 3 năm học 2016-2017) kèm theo lời giải chi tiết, mong nhận được cách làm khác và khai thác được máy tính trong quá trình làm bài.
Bài toán: Xét số phức $z$ thỏa mãn $\left| z+2-i \right|+\left| z-4-7i \right|=6\sqrt{2}$ . Gọi $m$ ,$M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của $\left| z-1+i \right|$ . Tính $P=m+M$.
A. $P=\sqrt{13}+\sqrt{73}$.
B. $P=\dfrac{5\sqrt{2}+2\sqrt{73}}{2}$.
C.$P=5\sqrt{2}+2\sqrt{73}$ .
D.$P=\dfrac{5\sqrt{2}+\sqrt{73}}{2}$ .
Phương pháp: Từ biểu thức số phức z ban đầu, phỏng đoán đường thẳng
Đáp án B.
Goi $M\left( x;y \right)$ là điểm biểu diễn của $z$.
Biến đổi :
[latex]\begin{align} & \left| z+2-i \right|+\left| z-4-7i \right|=6\sqrt{2} \nonumber \\ & \Leftrightarrow \left| \left( x+2 \right)+\left( y-1 \right)i \right|+\left| \left( x-4 \right)+\left( y-7 \right)i \right|=6\sqrt{2} \nonumber \\ & \Leftrightarrow \sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}+\sqrt{{{\left( x-4 \right)}^{2}}+{{\left( y-7 \right)}^{2}}}=6\sqrt{2} \nonumber \\ \nonumber \end{align}[/latex]Thử nhập phương trình $\sqrt{{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}}+\sqrt{{{\left( x-4 \right)}^{2}}+{{\left( y-7 \right)}^{2}}}=6\sqrt{2}$ vào máy, tìm nghiệm cho một vài giá trị nhỏ:
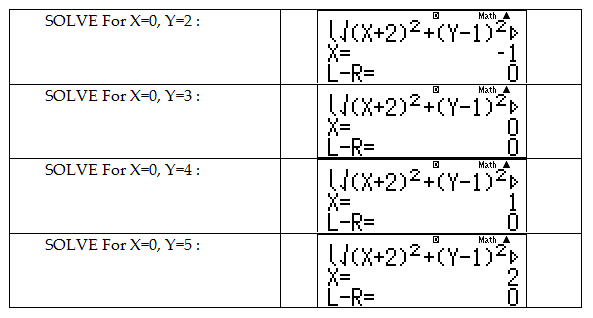
Phỏng đoán $M$ thuộc đoạn thẳng $AB$ với $A\left( -2;1 \right)$ , $B\left( 4,7 \right)$. Một đường thẳng có phương trình $y=x+3$ ,$x\in \left[ -2;4 \right]$ thỏa mãn. Đây là mấu chốt xử lí của bài toán, điều này không dễ để quan sát.
Từ đây ta có hai cách làm sau:
Cách 1: Từ biểu thức $\left| z-1+i \right|$, đặt $C\left( 1;-1 \right)$.
Ta có $\left| z+2-i \right|+\left| z-4-7i \right|=6\sqrt{2}$$\Leftrightarrow MA+MB=6\sqrt{2}$, mà $AB=6\sqrt{2}$ $\Rightarrow MA+MB=AB$.
Ta có
$\left| z-1+i \right|=MC\Rightarrow {{\left| z-1+i \right|}^{2}}=M{{C}^{2}}={{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}={{\left( x-1 \right)}^{2}}+{{\left( x+4 \right)}^{2}}=2{{x}^{2}}+6x+17$
Đặt $f\left( x \right)=2{{x}^{2}}+6x+17$ , $x\in \left[ -2;4 \right]$
${f}’\left( x \right)=4x+6$ ,${f}’\left( x \right)=0\Leftrightarrow x=-\dfrac{3}{2}$ ( nhận )
Ta có $f\left( -2 \right)=13$ ,$f\left( -\dfrac{3}{2} \right)=\dfrac{25}{2}$ ,$f\left( 4 \right)=73$ .
Vậy $f{{\left( x \right)}_{\max }}=f\left( 4 \right)=73$ , $f{{\left( x \right)}_{\min }}=f\left( -\dfrac{3}{2} \right)=\dfrac{25}{2}$ .
$\Rightarrow M=\sqrt{73}$ ,$m=\frac{5\sqrt{2}}{2}$ .$\Rightarrow P=\frac{5\sqrt{2}+2\sqrt{73}}{2}$ . Chọn B.
Cách 2: Biến đổi biểu thức thứ hai:
$\left| z-1+i \right|=\left| x+yi-1+i \right|=\left| \left( x-1 \right)+\left( y+1 \right)i \right|=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}\overset{y=x+3}{\mathop{=}}\,\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( x+4 \right)}^{2}}}$
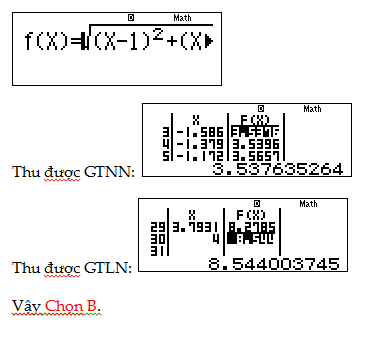
Nhập vào TABLE hàm số $f\left( x \right)=\sqrt{{{\left( x-1 \right)}^{2}}+{{\left( x+4 \right)}^{2}}}\text{, x}\in \left[ -2;4 \right]\text{ }$
Khảo sát hàm số này trên đoạn từ -2, tới 4 với bước nhảy $Step=\dfrac{6}{29}$.
About TailieuCasio
