BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Đa thức
- 20/11/2017
- 511 lượt xem
Cho f(x) = . Tính S =
Diễn đàn trả lời:
Tổng được viết lại:
$S=f\left( \dfrac{1}{2000} \right)+f\left( \dfrac{2}{2000} \right)+f\left( \dfrac{3}{2000} \right)+…+f\left( \dfrac{1999}{2000} \right)$
Nhận thấy $f\left( x \right)+f\left( 1-x \right)=1$. Có thể thử một vài giá trị bằng máy tính để dự đoán điều này.
Vậy
[latex]\begin{align} & S=\left[ f\left( \dfrac{1}{2000} \right)+f\left( \dfrac{1999}{2000} \right) \right]+\left[ f\left( \dfrac{2}{2000} \right)+f\left( \dfrac{1998}{2000} \right) \right]+…+\left[ f\left( \dfrac{999}{2000} \right)+f\left( \dfrac{1001}{2000} \right) \right]+f\left( \dfrac{1000}{2000} \right) \\ & S=999+f\left( \dfrac{1000}{2000} \right) \\ & S=\dfrac{1999}{2} \\ \end{align}[/latex]Tính trên máy tính:
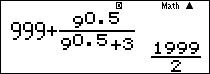
Chia sẻ
About Hakabaki Tokito
