BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
CÁC BÀI TOÁN ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH MẶT PHẲNG
- 12/12/2018
- 7,945 lượt xem
Tính diện tích mặt phẳng là một phần quan trọng trong chuyên đề tích phân thường xuất hiện trong các đề thi toán lớp 12 cũng như kỳ thi Quốc gia. Trong bài viết này, Diễn Đàn Máy Tính Cầm Tay chúng tôi sẽ hướng dẫn cách sử dụng máy tính Casio fx 580vnx để có thể tính nhanh, chính xác DIỆN TÍCH MẶT PHẲNG giới hạn bởi các đồ thị hàm số thông qua một vài ví dụ.
- Phần đầu tiên chúng tôi sẽ tóm tắt các công thức sử dụng tích phân tính diện tích mặt phẳng.
Bài toán 1: Diện tích của mặt phẳng giới hạn bởi $latex ({{C}_{1}}):y=f(x);({{C}_{2}}):y=g(x);x=a;x=b$ và $latex \left( a<b \right)$
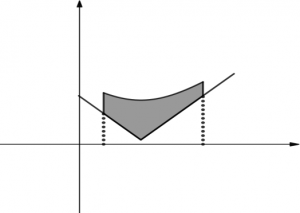
Công thức:
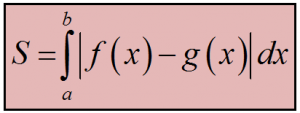
Bài toán 2: Diện tích hình phẳng giới hạn bởi $latex ({{C}_{1}}):y=f(x);({{C}_{2}}):y=g(x)$ và $latex ({{C}_{3}}):y=h(x)$
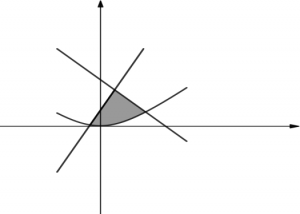
Bước 1: Tìm giao điểm của các đồ thị bằng cách giải các phương trình hoành độ giao điểm
Bước 2: Áp dụng công thức
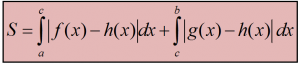
- Ở phần tiếp theo này, chúng tôi sẽ hướng dẫn sử dụng Casio fx 580vnx để giải các ví dụ cụ thể
Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $latex y={{x}^{2}}-2x$ , trục hoành và hai đường thẳng $latex x=2;x=0$
Hướng dẫn giải
Áp dụng công thức: $latex S=\int\limits_{0}^{2}{\left| {{x}^{2}}-2x \right|dx}$
Sử dụng máy tính Casio fx 580vnx để tính tích phân trên
yq([dp2[R0E2=
Ví dụ 2: Tính diện tích giới hạn bởi đồ thị của các hàm số $latex y=\frac{3x+5}{2x+2}$; $latex y=0$ ; $latex x=0$ và $latex x=2$
- $latex S=\ln 2+3$
- $latex S=\ln 3+3$
- $latex S=\ln 3$
- $latex S=\ln 3-2$
Hướng dẫn giải
Diện tích mặt phẳng cần tìm: $latex S=\int\limits_{0}^{2}{\left| \frac{3x+5}{2x+2} \right|}dx$
Quan sát đáp án ta thấy có 3 đáp án chứa $latex \ln 3$ nên ta tính $latex \int\limits_{0}^{2}{\left| \frac{3x+5}{2x+2} \right|}dx-\ln 3$
Sử dụng máy tính Casio fx 580vnx để tính biểu thức trên
yq(a3[+5R2[+2R0E2$ph3)=
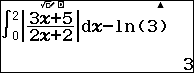
Đáp án: B
Ví dụ 3: Tính diện tích mặt phẳng giới hạn bởi đồ thị của các hàm số $latex ({{C}_{1}}):y={{x}^{2}}+1$;$latex ({{C}_{2}}):y={{x}^{2}}+2x$ ;$latex x=1$ và $latex x=2$
Hướng dẫn giải
Diện tích mặt phẳng cần tìm $latex S=\int\limits_{1}^{2}{\left| ({{x}^{2}}+1)-({{x}^{2}}+2x) \right|}dx$
Sử dụng máy tính Casio fx 580vnx để tính tích phân trên:
yq(([d+1)p([d+2[)R1E2=
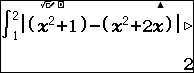
Ví dụ 4: Tính diện tích hình phẳng giới hạn bởi $latex ({{C}_{1}}):y={{x}^{2}}+2$và $latex ({{C}_{2}}):y=3x$
- $latex 2$
- $latex 3$
- $latex \frac{1}{2}$
- $latex \frac{1}{6}$
Hướng dẫn giải
Sử dụng máy tính Casio fx 580vnx để giải phương trình hoành độ giao điểm:
$latex {{x}^{2}}+2=3x\Leftrightarrow {{x}^{2}}-3x+2=0$
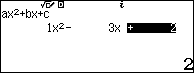
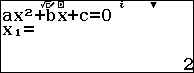
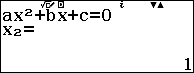
Khi đó : $latex S=\int\limits_{1}^{2}{\left| {{x}^{2}}-3x+2 \right|dx}$
Sử dụng máy tính CASIO fx-580VN X để tính tích phân trên:
yq([dp3[+2R1E2=
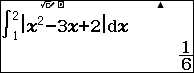
Đáp án : D
Ví dụ 5: Tính diện tích hình phẳng giới hạn bởi parabol $latex y=\sqrt{3}{{x}^{2}}$ , cung tròn có phương trình $latex y=\sqrt{4-{{x}^{2}}}$ ( với $latex 0\le x\le 2$ ) và trục hoành (như hình vẽ)
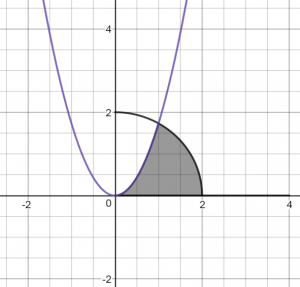
- $latex \frac{4\pi +\sqrt{3}}{12}$
- $latex \frac{4\pi -\sqrt{3}}{6}$
- $latex \frac{4\pi +2\sqrt{3}-3}{6}$
- $latex \frac{5\sqrt{3}-2\pi }{3}$
Hướng dẫn giải
Sử dụng máy tính Casio fx 580vnx tìm nghiệm của các phương trình hoành độ giao điểm
- $latex \sqrt{3}{{x}^{2}}=\sqrt{4-{{x}^{2}}}\Leftrightarrow 3{{x}^{4}}+{{x}^{2}}-4=0$ ($latex 0\le x\le 2$ ) $latex \Rightarrow x=1$
- $latex \sqrt{3}{{x}^{2}}=0\Rightarrow x=0$
- $latex \sqrt{4-{{x}^{2}}}=0$ ($latex 0\le x\le 2$) $latex \Rightarrow x=2$
Như vậy: Diện tích cần tìm
$latex S=\int\limits_{0}^{1}{\sqrt{3}{{x}^{2}}}dx+\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}}dx$
Sử dụng máy tính Casio fx 580vnx để tính tích phân trên và lưu kết quả:
ys3$[dR0E1$+ys4p[dR1E2Jz
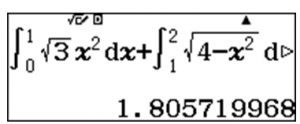
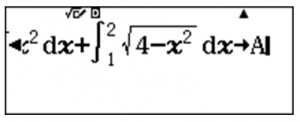
Thử các kết của đề bài ta có
About Ngọc Hiền Bitex
