Bài toán mức độ 1 về Liên phân số

Đề bài: Tìm số [latex]a[/latex] và [latex]b[/latex] biết rằng:

[latex]B=\frac{329}{1051}=\frac{1}{3+\frac{1}{5+\frac{1}{a+\frac{1}{b}}}}[/latex]

Bài giải:

Phân tích [latex]\frac{329}{1051}[/latex] dưới dạng liên phân số qua các bước:

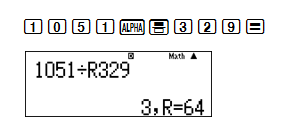
+Bước 1: Tìm nghịch đảo của phân số [latex]\frac{329}{1051}[/latex] và phân tích số 1051:

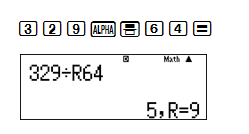
[latex]\frac{329}{1051}=\frac{1}{\frac{1051}{329}}=\frac{1}{3+\frac{64}{329}}[/latex]

+Bước 2: Tìm nghịch đảo của phân số \frac{64}{329} và phân tích 329 bằng phím :R:

Ta được:

[latex]\frac{329}{1051}=\frac{1}{\frac{1051}{329}}=\frac{1}{3+\frac{1}{5+\frac{9}{64}}}[/latex]

+Bước 3: Tiếp tục như vậy cho tới khi số dư nhận được [latex]R=0[/latex]:

[latex]\frac{329}{1051}=\frac{1}{\frac{1051}{329}}=\frac{1}{3+\frac{1}{5+\frac{1}{7+\frac{1}{9}}}}[/latex]

Kết luận: [latex]a=7;b=9[/latex]

Chia sẻ

BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay