BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
SỬ DỤNG HỆ THỨC LƯỢNG TRONG TAM GIÁC ĐỂ GIẢI QUYẾT CÁC BÀI TOÁN THỰC TẾ
- 19/12/2018
- 12,821 lượt xem
Tiếp nối các bài viết trong Chuyên đề Hệ thức lượng trong tam giác, bài viết này sẽ trình bày các bài toán thực tế liên quan đến hệ thức lượng trong tam giác. Qua đó giúp học sinh rèn luyện kỹ năng tính toán, vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Dưới đây là một số ví dụ minh họa:
Bài toán 1: Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang $latex {{35}^{o}}$ và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang $latex {{15}^{o}}$. Áp dụng hệ thức lượng trong tam giác tính chiều cao ngọn núi đó biết rằng tòa nhà cao $latex 60\left ( m \right)$
Hướng dẫn giải:
Gọi: $latex A,B$ lần lượt là vị trí của người đó tại tầng trệt và sân thượng. Như vậy ta có $latex AB=60$
$latex C,D$ lần lượt là đỉnh và chân của ngọn núi.
Bài toán được mô phỏng lại như hình vẽ
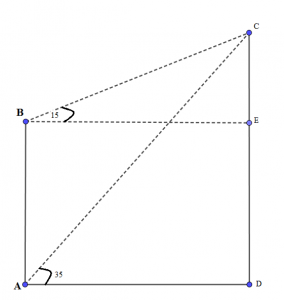
Ta có
$latex \widehat{CBA}=\widehat{CBE}+\widehat{EBA}={{90}^{0}}+{{15}^{0}}={{105}^{0}}$
$latex \widehat{BAC}=\widehat{BAD}-\widehat{CAD}={{90}^{0}}-{{35}^{0}}={{55}^{0}}$
$latex \widehat{BCA}={{180}^{0}}-\left( \widehat{CBA}-\widehat{BAC} \right)={{20}^{0}}$
Áp dụng định lý hàm sin vào $latex \Delta CBA$ ta có
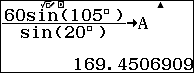
$latex \dfrac{AB}{\sin \left( \widehat{BCA} \right)}=\dfrac{AC}{\sin \left( \widehat{CBA} \right)}\Rightarrow AC=\dfrac{AB\sin \left( \widehat{CBA} \right)}{\sin \left( \widehat{BCA} \right)}=\dfrac{60\sin \left( {{105}^{0}} \right)}{\sin \left( {{20}^{0}} \right)}$
Sử dụng Casio fx 580vnx tính phép toán trên và lưu kết quả cạnh AC vào ô nhớ A
Xét $latex \Delta CAD$ vuông tại D ta có:
$latex CD=AC\sin \left( \widehat{CAD} \right)=A\sin \left( {{35}^{0}} \right)$
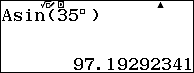
Vậy ngọn núi nhân tạo cao xấp xỉ $latex 97.193\left( m \right)$
Bài toán 2: Một ô tô muốn đi từ A đến C nhưng giữa A và C là một ngọn núi cao nên ô tô phải đi thành hai đoạn từ A đến B rồi từ B đến C, các đoạn đường tạo thành tam giác ABC có $latex AB=15km$, $latex BC=10km$ và $latex \widehat{ABC}={{105}^{0}}$. Giả sử cứ chạy $latex 1\left( km \right)$ ô tô tốn $latex 0.5\left( l \right)$ dầu.
- Tính số dầu ô tô phải tiêu thụ khi chạy từ A đến C mà phải qua B
- Giả sử người ta làm một đường hầm xuyên núi chạy thẳng từ A đến C thì khi đó ô tô chạy trên con đường mới này sẽ tiết kiệm được bao nhiêu chi phí đi lại so với đường cũ biết rằng giá của $latex 1\left( l \right)$ dầu là 16000 (đồng)
Hướng dẫn giải:
Bài toán được vẽ lại như sau:
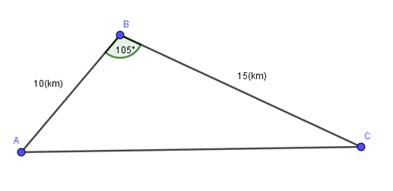
Câu a
Tổng độ dài đoạn đường khi đi từ A đến C qua B là $latex S=AB+BC=25\left( km \right)$
Vậy số dầu ô tô phải tiêu thụ khi chạy từ A đến C mà phải qua B: $latex 0.5S=12.5\left( l \right)$
Câu b:
Áp dụng định lý Cosin vào $latex \Delta ABC$ ta có:
$latex AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}-2.AB.BC\cos \left( \widehat{ABC} \right)}=\sqrt{{{15}^{2}}+{{10}^{2}}-2.15.10\cos \left( {{105}^{0}} \right)}$
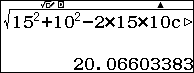
Số dầu ô tô phải tiêu thụ khi chạy thẳng từ A đến C là: $latex 0.5AC\left( l \right)$
Vậy ô tô chạy trên con đường mới này sẽ tiết kiệm được: $latex 16000\left( 12.5-0.5AC \right)\approx 39471.73$(đồng)
Cảm ơn các bạn đã theo dõi bài viết SỬ DỤNG HỆ THỨC LƯỢNG TRONG TAM GIÁC ĐỂ GIẢI QUYẾT CÁC BÀI TOÁN THỰC TẾ trên. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO.
keywords: hệ thức lượng trong tam giác, hệ thức lượng, toán thực tế.
About Ngọc Hiền Bitex
