BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Phần 2: Sử dụng lệnh solve để giải phương trình Pythagoras (Pitago) trên máy tính Casio fx-580VNX
- 12/03/2019
- 1,352 lượt xem
Trong toán học, định lý Pytago là một liên hệ căn bản trong hình học giữa ba cạnh của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại. đây là một lí thuyết quan trọng trong hình học nói riêng cũng như trong toán học nói chung. Loạt bài viết này sẽ chia sẽ kĩ thuật sử dụng Solve trên máy tính Casio fx-580VNX để giải phương trình Pythagoras nhanh chóng và chính xác hơn.
Trong toán học, định lý Pytago là một liên hệ căn bản trong hình học giữa ba cạnh của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại. đây là một lí thuyết quan trọng trong hình học nói riêng cũng như trong toán học nói chung. Loạt bài viết này sẽ chia sẽ kĩ thuật sử dụng Solve trên máy tính Casio fx-580VNX để giải phương trình Pythagoras nhanh chóng và chính xác hơn. Phần 2 này ad sẽ thêm một số bài tập để các bạn có thể luyện tập với nó nhiều hơn.
Link bài viết trước dành cho các bạn chưa xem: SỬ DỤNG LỆNH SOLVE ĐỂ GIẢI PHƯƠNG TRÌNH PYTHAGORAS TRÊN MÁY TÍNH CASIO FX-580VNX
Hoặc có thể xem video dưới đây:
2. Bài tập
Bài toán 4
Cho miếng vườn trồng cỏ hình chữ nhật $latex ABCD$ có chiều rộng $latex 6m $ và chiều dài bằng $latex \dfrac{4}{3}$ chiều rộng. Cột một con dê ở đỉnh A của miếng vườn hình chữ nhật.
a. Cần cột con dê bởi sợi dây dài bao nhiêu mét để có thể ăn cỏ ở vị trí xa nhất.
b. Biết rằng trồng $latex 1m^2 $ cỏ mỗi tháng thu hoạch được $latex 1,5 kg $ cỏ và mỗi ngày con dê tiêu thụ $latex 2kg $ cỏ tươi. Hỏi cỏ trong mảnh vườn có đủ cho con dê ăn trong 01 tháng không?
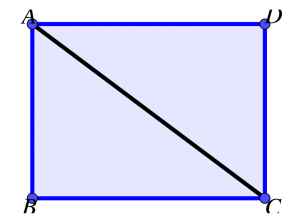
Hướng dẫn
a. Để con dê ăn cỏ ở vị trí xa nhất thì sợi dây dài bằng đoạn $ AC $.
\begin{equation}AB = \dfrac{4}{3}.6=8(m)\end{equation}
Áp dụng định lý Pythagoras trong tam giác $latex ABC $ vuông tại $latex B $. Ta có:
$$ AC^2 = AB^2 + BC^2 = 8^2 + 6^2 = 100 $$
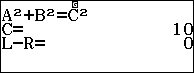
$latex \Rightarrow AC = 10m $
Vậy phải cột con dê bằng sợi dây dài $latex 10m $
b. Diện tích miếng vườn : $latex 6.8 = 48 (m^2) $
Số kg cỏ thu hoạch được là: $latex 48.1,5 = 72 (kg) $
Số cỏ đủ cho dê ăn trong: $latex 72:2 = 36 (\text{ngày})$
Vậy số cỏ đủ cho dê ăn trong $latex 01 $ tháng.
Bài toán 5
Bạn An đi từ nhà đến trường theo con đường (như hình vẽ)
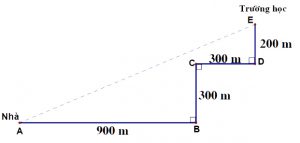Từ $latex A\to B\to C\to D\to E$. Biết $latex AB=900m,BC=300m,CD=300m,DE=200m$. Hỏi khoảng cách $latex AE$ dài bao nhiêu mét.
Hướng dẫn
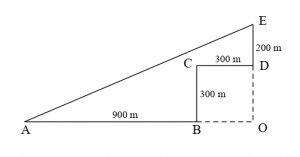
Gọi $latex O$ là giao điểm của $latex AB$ và $latex DE$
\begin{align}& AO=AB+BO=900+300=1200\left( m \right) \\ & EO=ED+DO=200+300=500\left( m \right) \\ \end{align}
Áp dụng định lý Pythagoras:
$latex A{{E}^{2}}=A{{O}^{2}}+E{{O}^{2}}={{1200}^{2}}+{{500}^{2}}=1690000$
$latex \Rightarrow AE=\sqrt{1690000}=1300\left( m \right)$
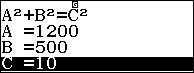
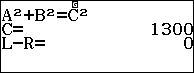
Vậy khoảng cách từ nhà bạn An đến trường là $latex 1300\left( m \right)$
Bài toán 6
Một khu đất hình tam giác vuông được bao quanh bởi ba con đường. Trên khu đất này có đánh dấu bốn địa điểm $latex A, B, C, D $ như hình vẽ. Biết các khoảng cách $$ AB = BC = x (km) ; CD = 1 (km); AD = 2 (km)$$ Học sinh không cần vẽ lại hình, hãy tính diện tích khu đất là bao nhiêu $latex (m^2) $?
Hướng dẫn
Áp dụng định lý Pythagoras cho tam giác $latex ABD$, ta được:
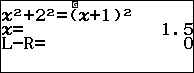
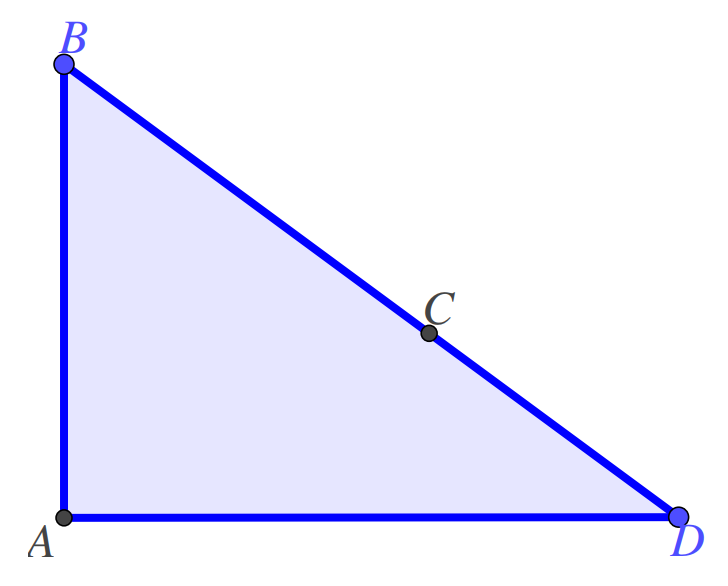
\begin{align}&{{x}^{2}}+{{2}^{2}}={{\left( x+1 \right)}^{2}}\\\Rightarrow &{{x}^{2}}+4={{x}^{2}}+2x+1\\\Rightarrow &x=\dfrac{3}{2}\end{align}
Vậy diện tích khu đất là:
\begin{equation*}{{S}_{ABD}}=\dfrac{1}{2}.AB.AD=\dfrac{1}{2}.\dfrac{3}{2}.2=\dfrac{3}{2}\left( {{m}^{2}} \right)\end{equation*}
———————————————————–
Trên đây là một số bài tập về phương trình Pythagoras nhằm giúp các em hiểu rõ hơn về tính năng của máy tính Casio fx-580VNX và tính toán các bài toán nhiều ẩn số một cách chính xác hơn. Bài viết khó tránh khỏi thiếu sót, các bạn có đóng góp gì thì cmt hoặc gửi tin nhắn qua fanpage nhé. Trân trọng.
About Bitex Khánh Vũ
