BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
HƯỚNG DẪN GIẢI CÂU 23 ĐỀ THI THỬ MÔN TOÁN THPT QUỐC GIA CHUYÊN ĐẠI HỌC VINH LẦN 3
- 02/06/2019
- 391 lượt xem
Bài viết này trình bày lời giải cho câu 23 trích từ đề thi thử môn Toán chuyên Đại học Vinh lần 3 về bài toán đường tiệm cận cùng với những phân tích rất chi tiết của TS. Nguyễn Thái Sơn
Để chuẩn bị cho kì thi THPT Quốc Gia 2019 chuẩn bị diễn ra, Diễn đàn máy tính cầm tay sẽ cùng các bạn ôn tập với những đề thi thử hay của các trường trong cả nước dưới sự hỗ trợ của máy tính Casio fx- 580 vnx. Trong bài viết này, chúng tôi sẽ gửi đến bạn đọc lời giải cho câu 23 trích từ đề thi thử môn Toán chuyên Đại học Vinh lần 3 về bài toán đường tiệm cận cùng với những phân tích rất chi tiết của TS. Nguyễn Thái Sơn.
Đề bài (trích đề thi thử môn Toán chuyên Đại học Vinh lần 3)
[dropshadowbox align=”none” effect=”lifted-both” width=”auto” height=”” background_color=”#ffffff” border_width=”1″ border_color=”#dddddd” ]Đồ thị hàm số $y=\dfrac{x+\sqrt{x^{2}+1}}{x-1}$ có bao nhiêu tiệm cận
- $2$.
- $3$.
- $4$.
- $1$.
[/dropshadowbox]
Hướng dẫn giải
Đối với bài toán này, chúng ta có thể sử dụng định nghĩa kết hợp với máy tính cầm tay để tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số.
Cho $x-1=0 \Rightarrow x=1$. Thay $x=1$ vào tử số của $y$ ta được kết quả là $1+\sqrt{2}$
Suy ra $x=1$ là tiệm cận đứng của $y$.
Để tìm các tiệm cận ngang của đồ thị hàm số $y$ ta sử dụng máy tính Casio fx– 580VN X để tìm giới hạn của hàm số $y=\dfrac{x+\sqrt{x^{2}+1}}{x-1}$
- Bước 1: Nhập vào biểu thức $\dfrac{x+\sqrt{x^{2}+1}}{x-1}$
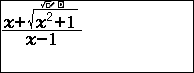
- Bước 2: Tính giá trị biểu thức tại $10^{10}$
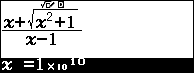
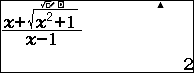
Như vậy $y=2$ là một tiệm cận ngang của đồ thị hàm số $y$
- Bước 3: Tính giá trị biểu thức tại $-10^{10}$
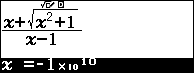
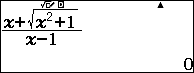
Như vậy $y=0$ là một tiệm cận ngang của đồ thị hàm số $y$
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Đáp án B
Để có thêm những phân tích sâu về dạng bài toán trên cũng như quy trình sử dụng máy tính Casio fx- 580VN X, bạn đọc có thể tham khảo thêm bài giảng của TS. Nguyễn Thái Sơn
Trong bài viết tiếp theo Diễn đàn máy tính cầm tay sẽ gửi đến bạn đọc cách sử dụng máy tính Casio để giải quyết bài toán về phương trình nghiệm phức phức thông qua câu 28 của đề thi thử môn Toán chuyên Đại học Vinh lần 3 dưới sự hướng dẫn của TS. Nguyễn Thái Sơn.
About Ngọc Hiền Bitex
