BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
QUY TẮC 72
- 17/02/2021
- 84 lượt xem
| Giả sử ta có một khoản đầu tư với giá trị hiện tại là $P$ và dự định mở một tài khoản ngân hàng với lãi suất hàng năm là $i$. Ta muốn tính thời gian để giá trị tương lai gấp đôi giá trị hiện tai, nghĩa là $F=2P$. Giả sử $\quad 5\%\leqslant i\leqslant 12\%\quad $ là lãi suất phổ biến ở nước ta. |
Xét phương trình: $$F=P(1+i)^n$$ trong đó $n$ là số kỳ hạn tính bằng năm và $i$ là lãi kép tính trên một năm. $i$ là một số thập phân và $I=100i$ là số đứng trước dấu % của $i$.
Từ phương trình trên ta suy ra $\dfrac{F}{P}=(1+i)^n$.
$F=2P \Leftrightarrow n=\log_{1+i}2$.
Ta muốn tính $nI=100i.\log_{1+i}2$. Muốn vậy ta xét hàm số $f(x)=100x\log_{1+x}2$.
Sử dụng tính năng lập bảng cho hàm số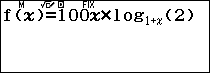 
Phạm vi của $i$ thuộc đoạn $[0,05;0,12]$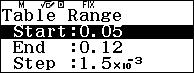 
Kết quả $nI\approx 72$ với mọi $i$ thuộc đoạn $[6,43\%; 9,29\%] $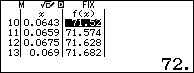 
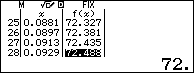
Chính xác hơn ta có: $nI\approx 72$ với mọi $i$ thuộc đoạn $[6,38\%; 9,32\%] $
| Kết luận: Với các tổ chức tín dụng chấp nhận lãi suất từ 6,38% đến 9,32% thì $nI$ luôn luôn bằng 72.
|
Ví dụ: (Sách nhập môn Toán Tài Chính của tác giả Nguyễn Tiến Dũng và Đỗ Đức Thái)
Bài tập 4.6. Cần bao lâu để tăng vốn lên gấp đôi nếu lợi suất là 6%/năm ?
Trả lời nhanh 12 năm. (Nếu lấy 71, kết quả sẽ là 11,83 $\approx 12$)
Bài tập 4.7. Nếu một khoản tiền gửi, được tính lãi kép theo năm, tăng lên gấp đôi sau 10 năm, thì mức lợi suất (lãi kép theo năm) của nó là bao nhiêu?
Trả lời nhanh 7,2%.
Phụ lục:
So sánh lãi suất ngân hàng nào cao nhất tháng 2/2021
|
STT |
Ngân hàng |
LS cao nhất |
Điều kiện |
|
1 |
Eximbank |
8,40% |
13, 24 tháng (từ 500 tỷ trở lên) |
|
2 |
ABBank |
8,30% |
13 tháng |
|
3 |
Ngân hàng OCB |
8,20% |
13 tháng, 500 tỷ đồng trở lên |
|
4 |
VietBank |
7,80% |
13 tháng |
|
5 |
ACB |
7,40% |
13 tháng, từ 30 tỷ trở lên |
|
6 |
SCB |
7,30% |
12 tháng, từ 500 tỷ đồng |
|
7 |
Ngân hàng Việt Á |
7,20% |
15 – 36 tháng |
|
8 |
Kienlongbank |
7,10% |
Từ 13 đến 60 tháng |
|
9 |
Techcombank |
7,10% |
12 tháng, 200 tỷ trở lên |
|
10 |
MSB |
7,00% |
12 tháng, 13 tháng (200 tỷ trở lên) |
|
11 |
LienVietPostBank |
6,99% |
13 tháng (từ 300 tỷ trở lên) và 60 tháng |
|
12 |
HDBank |
6,95% |
13 tháng, 300 tỷ trở lên |
|
13 |
Sacombank |
6,95% |
13 tháng, Từ 500 tỷ trở lên |
|
14 |
MBBank |
6,90% |
24 tháng, từ 200 đến dưới 300 tỷ |
|
15 |
SeABank |
6,88% |
36 tháng, Từ 10 tỷ trở lên |
|
16 |
OceanBank |
6,80% |
18, 24, 36 tháng |
|
17 |
PVcomBank |
6,80% |
24, 36 tháng |
|
18 |
Ngân hàng Bản Việt |
6,80% |
60 tháng |
|
19 |
Ngân hàng Quốc dân (NCB) |
6,75% |
18 – 36 tháng |
|
20 |
Ngân hàng Bắc Á |
6,70% |
18, 24, 36 tháng |
|
21 |
TPBank |
6,60% |
18, 36 tháng |
|
22 |
Ngân hàng Đông Á |
6,50% |
13 tháng |
|
23 |
Saigonbank |
6,50% |
13 – 36 tháng |
|
24 |
SHB |
6,40% |
24 tháng trở lên, từ 2 tỷ đến 500 tỷ |
|
25 |
VIB |
6,20% |
24 và 36 tháng, từ 1 tỷ trở lên |
|
26 |
Agribank |
5,60% |
12 tháng đến 24 tháng |
|
27 |
VietinBank |
5,60% |
Từ 12 tháng trở lên |
|
28 |
BIDV |
5,60% |
12 – 36 tháng |
|
29 |
Vietcombank |
5,50% |
12 tháng |
|
30 |
VPBank |
5,50% |
24, 36 tháng, Từ 50 tỷ trở lên |
Nguồn: Ngọc Mai tổng hợp
About TS. Nguyễn Thái Sơn
