BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải câu 44 chuyên Vinh lần 2
- 31/05/2021
- 129 lượt xem
Đây là bài toán vận dụng cao, dành cho học sinh khá giỏi. Nếu giải bằng PP truyền tống sẽ mất rất nhiều thời gian, do đó thầy đề xuất công thức (đã được chứng minh trên diễn đàn bitexedu) sau đó sử dụng MTCT, và chỉ có máy tính mới giải được phương trình thiết lập được trong vòng 60 giây.
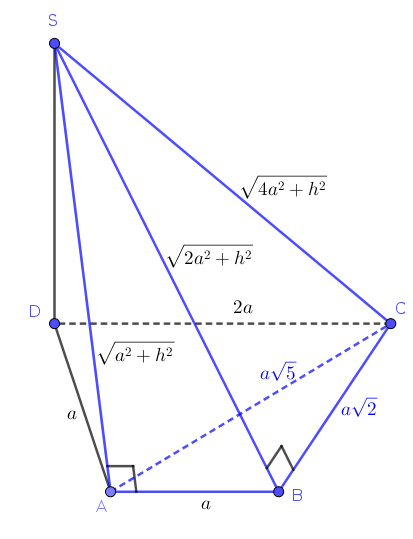
Gọi $h$ là chiều cao của khối chóp $SABCD$. Độ dài các cạnh của khối tứ diện SABC như hình vẽ. Chọn $a$ làm 1 (đvd).
Ta có công thức tìm góc tạo bởi hai mặt bên của một khối tứ diện. Cụ thể ở đây là hai mặt phẳng $(SBA)$ và $(SBC)$ với giao tuyến $SB$ và cạnh đối diện của nó là $AC$.
$$\cos 30^\circ=\dfrac{\left|SB^2(AB^2+AS^2+CB^2+CS^2-SB^2-2AC^2)-(AB^2-AS^2)(CB^2-CS^2)\right|}{16S_{SBA}.S_{SBC}}$$
$$\cos 30^\circ=\dfrac{\left|SB^2(\underbrace{AB^2+AS^2+CB^2+CS^2}_{\text{tổng bình phương của 4 cạnh}}-SB^2-2AC^2)-\underbrace{(AB^2-AS^2)(CB^2-CS^2)}_{\text{tích của hiệu bình phương hai cạnh đúng thứ tự}}\right|}{16S_{SBA}.S_{SBC}}$$
- Viết lên màn hình
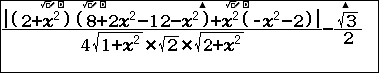
- Bấm SHIFT SOLVE nhập $x$ tuỳ ý
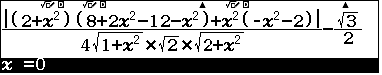
- Nhấn = xuất ta nghiệm
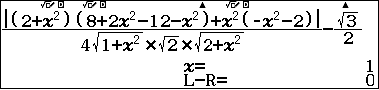
Vậy $h=a$, suy ra $V_{\text{SABCD}}=\dfrac13\times \dfrac12\times 3a\times a\times a=\dfrac{a^3}{2}$, chọn D.
Cách nhớ công thức:
- 1. Khối tứ diện có 6 cạnh, chia ra 3 cặp cạnh đối.
- 2. Bỏ đi giao tuyến và cạnh đối diện với giao tuyến, còn lại 4 cạnh.
- 3. Công thức tập trung vào 4 cạnh này.
- 4. Các cạnh còn lại và hai diện tích phải nhớ.
About TS. Nguyễn Thái Sơn
