GIẢI CÁC CÂU VẬN DỤNG CAO TRONG ĐỀ THI THỬ NGÀY 10/07/2020
- 20/07/2020
- 118 lượt xem
Nhằm giúp các bạn ôn luyện tốt hơn, thay vì chỉ đăng đáp án như trước thì đợt này Diễn đàn sẽ thực hiện giải một số câu trong đề thi trên máy tính Casio fx-580VN X. Hi vọng nó sẽ giúp ích được các bạn trong kì thi tuyển sinh THPT QG 2020 sắp tới. Trong bài viết này Diễn đàn sẽ thực hiện giải 10 câu cuối của đề thi.
LINK: http://bitexedu.com/de-thi-thu-ngay-10-07-2020/
Câu 41. Có bao nhiêu giá trị nguyên của tham số $m$ sao cho hàm số $f(x) = – \dfrac{1}{3}{x^3} + m{x^2} – 9x – 3$ nghịch biến trên $\mathbb{R}$?
| A. $7$. | B. $6$. |
| C. $5$. | D. $2$. |
Lời giải
Ta có $f'(x) = – {x^2} + 2mx – 9$
Hàm số nghịch biến trên $\mathbb{R}$ $ \Leftrightarrow f'(x) \leqslant 0,\forall x \in \mathbb{R}$ $ \Leftrightarrow \left\{ \begin{gathered} a = – 1 < 0 \hfill \\ \Delta ‘ = {m^2} – 9 \leqslant 0 \hfill \\\end{gathered} \right.$$ \Leftrightarrow m \in [ – 3;3]$
$m \in \mathbb{Z}$ $ \Rightarrow $$m \in \left\{ { – 3, – 2, – 1,0,1,2,3} \right\}$. Chọn câu A.
Câu 42. Số lượng của một loài vi khuẩn sau $t$ (giờ) được xấp xỉ bằng đẳng thức $Q = {Q_0}.{e^{0,195t}}$, trong đó ${Q_0}$ là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn ban đầu là $5000$ con thì sau bao lâu số lượng vi khuẩn là $100000$ con.
| A. $15,36$ giờ. | B. $3,55$ giờ. |
| C. $16,35$ giờ. | D. $20$ giờ. |
Lời giải
Chọn A
Ta có $100000 = 5000.{e^{0,195t}} \Leftrightarrow {e^{0,195t}} = 20 \Leftrightarrow 0,195t = \ln 20 \Leftrightarrow t \approx 15,36$.
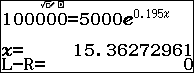
Câu 43. Cho hàm số $f(x) = \dfrac{{2 – ax}}{{bx – c}}$$\left( {a,b,c \in \mathbb{R},b \ne 0} \right)$ có bảng biến thiên như sau:
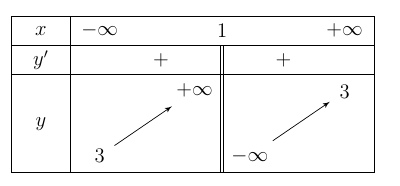
Tổng các số ${\left( {a + b + c} \right)^2}$ thuộc khoảng nào sau đây
| A. $\left( {1;2} \right)$. | B. $\left( {2;3} \right)$. |
| C. $\left( {0;\dfrac{4}{9}} \right)$. | D. $\left( {\dfrac{4}{9};1} \right)$. |
Lời giải
Ta có $\mathop {\lim }\limits_{x \to \infty } \dfrac{{2 – ax}}{{bx – c}} = \dfrac{{ – a}}{b}$, theo giả thiết suy ra $\dfrac{{ – a}}{b} = 3 \Leftrightarrow a = – 3b\left( 1 \right)$
Hàm số không xác định tại $x = 1 \Rightarrow b – c = 0 \Leftrightarrow b = c\left( 2 \right)$
Hàm số đồng biến trên từng khoảng xác định nên $f’\left( x \right) = \dfrac{{ac – 2b}}{{{{\left( {bx – c} \right)}^2}}} > 0$ với mọi $x$ khác 1
Suy ra $ac – 2b > 0 \Leftrightarrow – 3{b^2} – 2b > 0 \Leftrightarrow – \dfrac{2}{3} < b < 0$
Từ (1),(2) ta có ${\left( {a + b + c} \right)^2} = {\left( { – 3b + b + b} \right)^2} = {b^2}$ (4).
Áp dụng (3) vào (4) ta được: ${b^2} \in \left( {0;\dfrac{4}{9}} \right)$
Vậy tổng $a + b + c$ thuộc khoảng $\left( {0;\dfrac{4}{9}} \right)$. Chọn C.
Câu 44. Cho hình trụ có chiều cao bằng $8a$. Biết hai điểm $A,C$ lần lượt nằm trên hai đáy thỏa $AC = 10a$, khoảng cách giữa $AC$ và trục của hình trụ bằng $4a$. Thể tích của khối trụ đã cho là
| A. $128\pi {a^3}$. | B. $320\pi {a^3}$. |
| C. $80\pi {a^3}$. | D. $200\pi {a^3}$. |
Lời giải
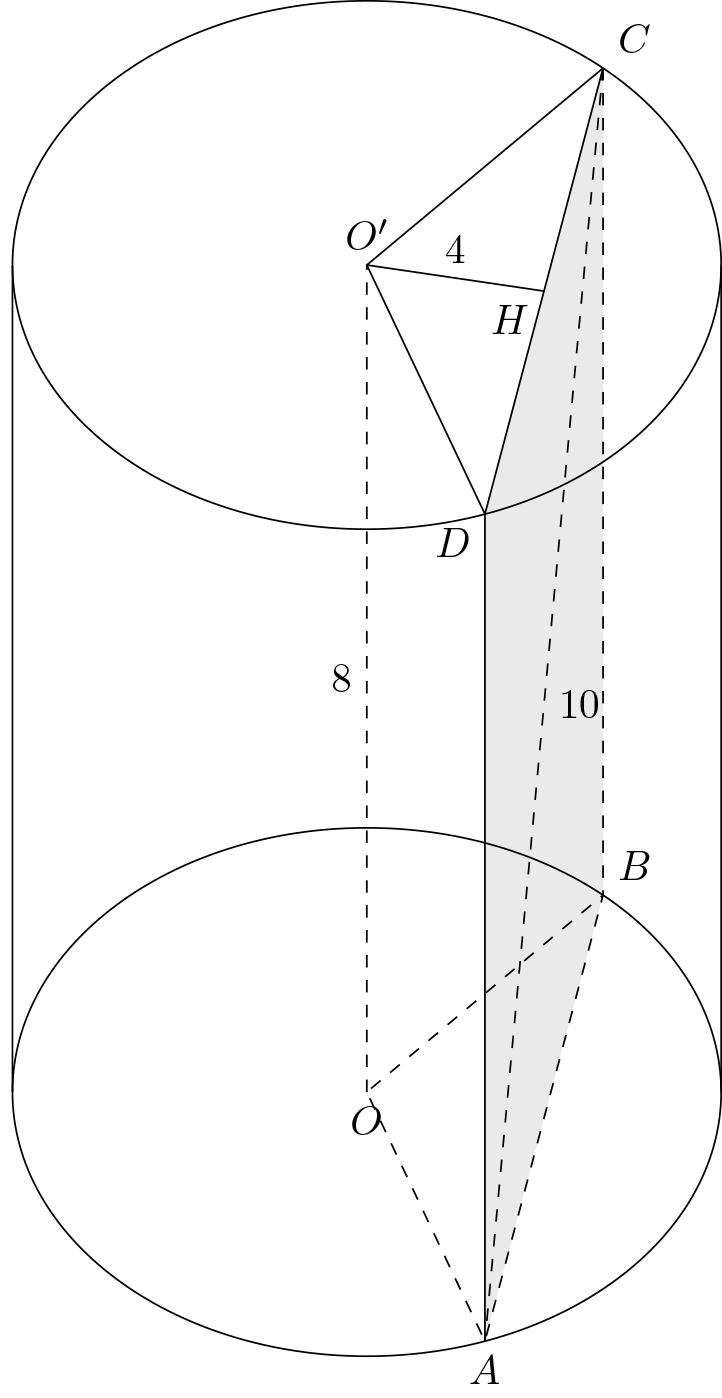
Gọi $\left( O \right),\left( {O’} \right)$ lần lượt là hai đường tròn đáy. $A \in \left( O \right),C \in \left( {O’} \right)$.
Dựng $AD,CB$ lần lượt song song với $OO’$ ($D \in \left( {O’} \right),B \in \left( O \right)$. Dễ dàng có $ABCD$ là hình chữ nhật.
Do $AC = 10a,AD = 8a \Rightarrow DC = 6a$.
Gọi $H$ là trung điểm của $DC$.
$\left\{ {\begin{array}{*{20}{c}}{O’H \bot DC} \\{O’H \bot AD}\end{array}} \right. \Rightarrow O’H \bot \left( {ABCD} \right)$.
Ta có $OO’//\left( {ABCD} \right)$$ \Rightarrow d\left( {OO’,AC} \right) = d\left( {OO’,\left( {ABCD} \right)} \right) = O’H = 4a$.
$O’H = 4a,CH = 3a \Rightarrow R = O’C = 5a$.
Vậy thể tích của khối trụ là $V = \pi {R^2}h = \pi {\left( {5a} \right)^2}8a = 200\pi {a^3}$. Chọn D.
Câu 45. Cho hàm số$f\left( x \right)$ có $f\left( 0 \right) = – 1$và $f’\left( x \right) = x\left( {6 + 12x + {e^{ – x}}} \right),\forall x \in \mathbb{R}$. Khi đó $\int\limits_0^1 {f\left( x \right)} {\text{d}}x$ bằng
| A. $3e$. | B. $3{e^{ – 1}}$. |
| C. $4 – 3{e^{ – 1}}$. | D. $ – 3{e^{ – 1}}$. |
Lời giải
Ta có: $f’\left( x \right) = x\left( {6 + 12x + {e^{ – x}}} \right),\forall x \in \mathbb{R}$ nên $f\left( x \right)$là một nguyên hàm của $f’\left( x \right)$.
$$\int {f’\left( x \right){\text{d}}x = \int {x\left( {6 + 12x + {e^{ – x}}} \right){\text{d}}x} } = \int {\left( {6x + 12{x^2}} \right){\text{d}}x + \int {x{e^{ – x}}{\text{d}}x} } $$
Mà $\int {\left( {6x + 12{x^2}} \right){\text{d}}x = 3{x^2} + 4{x^3}} + C$
Xét $\int {x{e^{ – x}}{\text{d}}x} $: Đặt $\left\{ \begin{gathered} u = x \hfill \\ {\text{d}}v = {e^{ – x}}{\text{d}}x \hfill \\\end{gathered} \right. \Rightarrow \left\{ \begin{gathered} {\text{d}}u = {\text{d}}x \hfill \\ v = – {e^{ – x}} \hfill \\\end{gathered} \right.$
$$\int {x{e^{ – x}}{\text{d}}x = – x{e^{ – x}} + \int {{e^{ – x}}} } {\text{d}}x = – x{e^{ – x}} – {e^{ – x}} + C = – \left( {x + 1} \right){e^{ – x}} + C$$
Suy ra $f\left( x \right) = 3{x^2} + 4{x^3} – \left( {x + 1} \right){e^{ – x}} + C,\forall x \in \mathbb{R}$.
Mà $f\left( 0 \right) = – 1 \Rightarrow C = 0$ nên $f\left( x \right) = 3{x^2} + 4{x^3} – \left( {x + 1} \right){e^{ – x}},\forall x \in \mathbb{R}$.
Sử dụng máy tính :
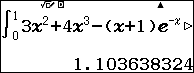



Vậy $\int\limits_0^1 {f\left( x \right)} {\text{d}}x = \int\limits_0^1 {\left( {3{x^2} + 4{x^3} – \left( {x + 1} \right){e^{ – x}}} \right)} {\text{d}}x = 3{{\text{e}}^{ – 1}}$
Chọn câu B.
Câu 46. Cho hàm số $f\left( x \right) = a{x^3} + b{x^2} + bx + c$ có đồ thị như hình vẽ:
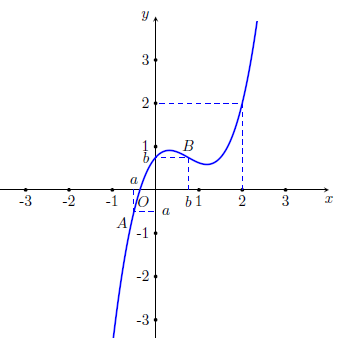
Số nghiệm nằm trong $\left( {\dfrac{{ – \pi }}{2};3\pi } \right)$ của phương trình $f\left( {\cos x + 1} \right) = \cos x + 1$ là
| A. $2$. | B. $3$. |
| C. $5$. | D. $4$. |
Lời giải
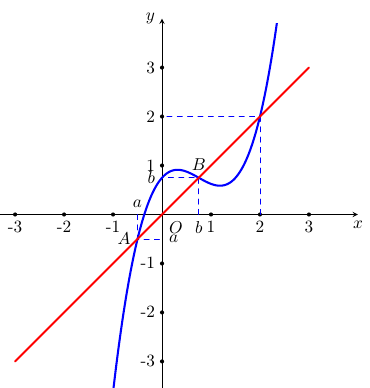
Từ đồ thị ta có $f\left( x \right) = x \Leftrightarrow \left[ \begin{gathered} x = a \in \left( { – \infty ;0} \right) \hfill \\ x = b \in \left( {0;1} \right) \hfill \\ x = 2 \hfill \\\end{gathered} \right.$
Do đó $f\left( {\cos x + 1} \right) = \cos x + 1$
$ \Leftrightarrow \left[ \begin{gathered} \cos x + 1 = a \in \left( { – \infty ;0} \right) \hfill \\ \cos x + 1 = b \in \left( {0;1} \right) \hfill \\ \cos x + 1 = 2 \hfill \\\end{gathered} \right.$
$ \Leftrightarrow \left[ \begin{gathered}\cos x = a – 1 = {t_1} \in \left( { – \infty ; – 1} \right)\,\,(VN) \hfill \\ \cos x = b – 1 = {t_2} \in \left( { – 1;0} \right)\,\,\,\,\,\,\,(1) \hfill \\\cos x = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \hfill \\\end{gathered} \right.$
Dựa vào đường tròn lượng giác, phương trình (1) có 3 nghiệm nằm trong $\left( {\dfrac{{ – \pi }}{2};3\pi } \right)$.
Phương trình (2) có $2$ nghiệm nằm trong $\left( {\dfrac{{ – \pi }}{2};3\pi } \right)$.
Vậy phương trình ban đầu có tất cả 5 nghiệm nằm trong $\left( {\dfrac{{ – \pi }}{2};3\pi } \right)$. Chọn câu C.
Câu 47. Xét các số thực dương $a$, $b$, $x$,$y$ thỏa mãn $a > 1$, $b > 1$và ${a^{2x}} = {b^{3y}} = a{}^6{b^6}$. Biết giá trị nhỏ nhất của biểu thức $P = 4xy + 2x – y$có dạng $m + n\sqrt {165} $(với $m,n$là các số tự nhiên), tính $S = m + n$.
| A. $58$. | B. $54$. |
| C. $56$. | D. $60$. |
Lời giải
Theo bài ra ta có: ${a^{2x}} = {b^{3y}} = {a^6}{b^6}$
$ \Leftrightarrow \left\{ \begin{gathered} {a^{2x}} = {a^6}{b^6} \hfill \\ {b^{3y}} = {a^6}{b^6} \hfill \\\end{gathered} \right.$
$ \Leftrightarrow \left\{ \begin{gathered} 2x = {\log _a}\left( {{a^6}{b^6}} \right) \hfill \\ 3y = {\log _b}\left( {{a^6}{b^6}} \right) \hfill \\\end{gathered} \right.$
$ \Leftrightarrow \left\{ \begin{gathered} 2x = 6 + 6{\log _a}b \hfill \\ 3y = 6 + 6{\log _b}a \hfill \\\end{gathered} \right.$
$ \Leftrightarrow \left\{ \begin{gathered} x = 3\left( {1 + {{\log }_a}b} \right) \hfill \\ y = 2\left( {1 + {{\log }_b}a} \right) \hfill \\\end{gathered} \right.$
Vì $a$, $b > 1$nên ${\log _a}b > {\log _a}1 = 0$.
Do đó:
$P = 4xy + 2x – y = 24(1 + {\log _a}b)(1 + {\log _b}a) + 6 + 6\log {}_ab – 2 – 2{\log _b}a$
$ = 52 + 30{\log _a}b + 22{\log _b}a \geqslant 52 + 2\sqrt {30{{\log }_a}b.22{{\log }_b}a} = 52 + 4\sqrt {165} $
Vậy $P$ đạt giá trị nhỏ nhất là $m + n\sqrt {165} $ khi $30{\log _a}b = 22{\log _b}a \Leftrightarrow {\log _a}b = \sqrt {\dfrac{{11}}{{15}}} \Leftrightarrow b = {a^{\sqrt {\frac{{11}}{{15}}} }}$
Ta có: $\left\{ \begin{gathered} m = 52 \hfill \\ n = 4 \hfill \\\end{gathered} \right. \Rightarrow m + n = 56$. Chọn C.
Câu 48. Cho hàm số $f\left( x \right) = \left| {3{e^{4x}} – 4{e^{3x}} – 24{e^{2x}} + 48{e^x} + m} \right|$. Gọi $A$, $B$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên $\left[ {0;\ln 2} \right]$.Gọi S là tập hợp tất cả các giá trị nguyên của tham số $m$thuộc $\left[ { – 23;10} \right)$ thỏa mãn $A \leqslant 3B$. Tổng các phần tử của tập S bằng
| A. $ – 33$. | B. $0$. |
| C. $ – 111$. | D. $ – 74$. |
Lời giải
Đặt $t = {e^x},x \in \left[ {0;\ln 2} \right] \Rightarrow t \in \left[ {1;2} \right]$
Xét hàm số $h\left( t \right) = |3{t^4} – 4{t^3} – 24{t^2} + 48t + m|$trên $\left[ {1;2} \right]$.
Đặt $g\left( t \right) = 3{t^4} – 4{t^3} – 24{t^2} + 48t + m$
$g’\left( t \right) = 12{t^3} – 12{t^2} – 48t + 48$; $g’\left( t \right) = 0$
$ \Leftrightarrow \left[ \begin{gathered}t = – 2 \notin [1;2] \hfill \\t = 2 \hfill \\t = 1 \hfill \\\end{gathered} \right.$;
$g\left( 1 \right) = m + 23$, $g\left( 2 \right) = m + 16$.
TH1:$ – 16 \leqslant m < 10$$ \Rightarrow m + 23 \geqslant m + 16 \geqslant 0$$ \Rightarrow A = \mathop {\max }\limits_{\left[ {1;2} \right]} h\left( t \right)$$ = m + 23$; $B = \mathop {\min }\limits_{\left[ {1;2} \right]} h\left( t \right)$$ = m + 16$.
Suy ra:: $\left\{ \begin{gathered}- 16 \leqslant m < 10 \hfill \\m + 23 \leqslant 3m + 48 \hfill \\\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}- 16 \leqslant m < 10 \hfill \\m \geqslant \dfrac{{ – 25}}{2} \hfill \\\end{gathered} \right.$
$ \Rightarrow \dfrac{{ – 25}}{2} \leqslant m < 10$.
Do đó: có $22$giá trị
TH2: $ – 23 \leqslant m < – 16$$ \Rightarrow \left| {m + 23} \right| = m + 23,{\text{ }}|m + 16| = – m – 16$.
Dễ thấy $B = 0$. Suy ra $\left[ \begin{gathered}\left\{ \begin{gathered}m + 23 < – m – 16 \hfill \\- m – 16 \leqslant 0 \hfill \\\end{gathered} \right. \hfill \\\left\{ \begin{gathered}m + 23 \geqslant – m – 16 \hfill \\m + 23 \leqslant 0 \hfill \\\end{gathered} \right. \hfill \\\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}- 16 \leqslant m < – 19.5 \hfill \\- 19.5 \leqslant m \leqslant – 23 \hfill \\\end{gathered} \right.(VL)$
Vậy $S = \left\{ { – 12; – 11;…;0;1;…\left. 9 \right\}} \right.$ và tổng các phần tử của tập S bằng $ – 12 + \left( { – 11} \right) + \left( { – 10} \right) = – 33$. Chọn A.
Câu 49. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $3$, chiều cao bằng $8$. Gọi $M$ là trung điểm $SB$, $N$ là điểm thuộc $SD$ sao cho $\overrightarrow {SN} = 2\overrightarrow {ND} $. Thể tích của tứ diện $ACMN$ bằng
| A. $V = 9$. | B. $V = 6$. |
| C. $V = 18$. | D. $V = 3$. |
Lời giải
Chọn B
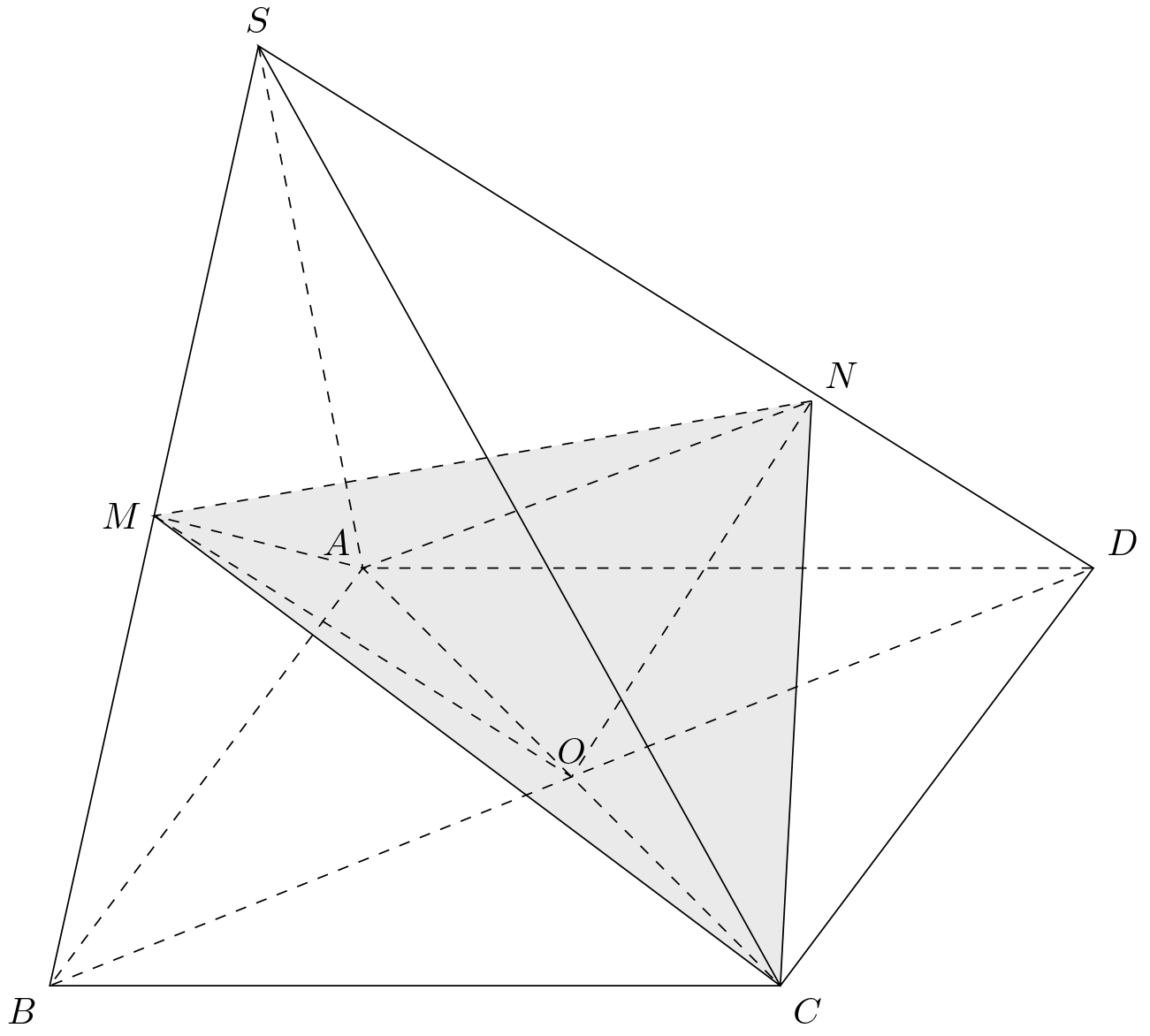
Ta có ${S_{ABCD}} = 9 \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}.9.8 = 24.$
$$ \Rightarrow {V_{S.ABD}} = \dfrac{1}{2}{V_{S.ABCD}} = 12;\,{V_{S.ABO}} = {V_{S.ADO}} = 6.$$
Vì $M$ là trung điểm $SB$, $N$ là điểm thuộc cạnh $SD$ sao cho $\overrightarrow {SN} = 2\overrightarrow {ND} $$ \Rightarrow \dfrac{{SM}}{{SB}} = \dfrac{1}{2},\,\dfrac{{SN}}{{SD}} = \dfrac{2}{3}$
+) $\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3} \Rightarrow {V_{S.AMN}} = \dfrac{1}{3}{V_{S.ABD}} = 4$
+) $\dfrac{{{V_{M.AOB}}}}{{{V_{S.AOB}}}} = \dfrac{{MB}}{{SB}} = \dfrac{1}{2} \Rightarrow {V_{M.AOB}} = \dfrac{1}{2}{V_{S.AOB}} = 3$
+) $\dfrac{{{V_{N.AOD}}}}{{{V_{S.AOD}}}} = \dfrac{{ND}}{{SD}} = \dfrac{1}{3} \Rightarrow {V_{N.AOD}} = \dfrac{1}{3}{V_{S.AOD}} = 2$
Ta có ${V_{C.AMN}} = 2{V_{O.AMN}} = 2\left( {{V_{S.ABD}} – {V_{S.AMN}} – {V_{M.AOB}} – {V_{N.AOD}}} \right)$
Vậy ${V_{C.AMN}} = 2{V_{O.AMN}} = 2\left( {12 – 4 – 3 – 2} \right) = 6$.
Câu 50. Có bao nhiêu số nguyên $y$ để tồn tại số thực $x$thỏa mãn ${\log _{11}}\left( {3{x} + 4y} \right) = {\log _4}\left( {{x^2} + {y^2}} \right)$?
| A. $3$. | B. $2$. |
| C. $1$. | D. Vô số. |
Lời giải
Chọn B
Đặt ${\log _{11}}\left( {3{x} + 4y} \right) = {\log _4}\left( {{x^2} + {y^2}} \right) = t \Leftrightarrow \left\{ \begin{gathered}3{x} + 4y = {11^t} \hfill \\{x^2} + {y^2} = {4^t} \hfill \\\end{gathered} \right.$ (*).
Hệ có nghiệm $ \Leftrightarrow $ đường thẳng $\Delta :3{x} + 4y = {11^t}$ và đường tròn có điểm chung $ \Leftrightarrow d\left( {O,\Delta } \right) \leqslant R \Leftrightarrow \dfrac{{{{11}^t}}}{5} \leqslant {2^t} \Leftrightarrow {\left( {\dfrac{{11}}{2}} \right)^t} \leqslant 5 \Leftrightarrow t \leqslant {\log _{\frac{{11}}{2}}}5$.
Do ${x^2} + {y^2} = {4^t}$ nên $\left| y \right| \leqslant {2^t} \leqslant {2^{{{\log }_{\frac{{11}}{2}}}5}} \approx 1.9239767$.
Vì $y \in \mathbb{Z}$ nên $y \in \left\{ { – 1;0;1} \right\}$.
Thử lại:
– Với $y = – 1$, hệ (*) trở thành
$\left\{ \begin{gathered}3{x} – 4 = {11^t} \hfill \\{x^2} + 1 = {4^t} \hfill \\\end{gathered} \right. \Rightarrow {\left( {\dfrac{{{{11}^t} + 4}}{3}} \right)^2} + 1 = {4^t} \Leftrightarrow {121^t} + {8.11^t} + 25 = {9.4^t}$ (**)
Nếu $t < 0$ thì ${4^t} < 1 \Rightarrow {4^t} < {\left( {\dfrac{{{{11}^t} + 4}}{3}} \right)^2} + 1$.
Nếu $t \geqslant 0 \Rightarrow \left\{ \begin{gathered}{121^t} \geqslant {4^t} \hfill \\{8.11^t} \geqslant {8.4^t} \hfill \\\end{gathered} \right. \Rightarrow {121^t} – {4^t} + 8\left( {{{11}^t} – {4^t}} \right) + 25 > 0$.
Vậy (**) vô nghiệm.
– Với $y = 0$ thì hệ (*) trở thành $\left\{ \begin{gathered}3x = {11^t} \hfill \\{x^2} = {4^t} \hfill \\\end{gathered} \right. \Rightarrow \dfrac{{{{121}^t}}}{9} = {4^t} \Leftrightarrow t = {\log _{\frac{{11}}{2}}}3 \Rightarrow x = \dfrac{{{{11}^{{{\log }_{\frac{{11}}{2}}}3}}}}{3}$.
– Với $y = 1$ thì hệ (*) trở thành $\left\{ \begin{gathered} 3{\text{x}} + 4 = {11^t} \hfill \\ {x^2} + 1 = {4^t} \hfill \\ \end{gathered} \right. \Rightarrow {\left( {\dfrac{{{{11}^t} – 4}}{3}} \right)^2} + 1 = {4^t} \Leftrightarrow {121^t} – {8.11^t} + 25 = {9.4^t}$
Xét hàm số $f(t) = {121^t} – {8.11^t} + 25 – {9.4^t}$, liên tục trên $\left[ {\dfrac{1}{2};1} \right]$ có $f\left( {\dfrac{1}{2}} \right)f\left( 1 \right) < 0$ nên phương trình $f(t) = 0$ luôn có nghiệm thuộc đoạn $\left[ {\dfrac{1}{2};1} \right]$. Khi đó hiển nhiên sẽ tồn tại x thỏa mãn.
Vậy có 2 giá trị nguyên của $y$ thỏa mãn là $y = 0,\,\,\,y = 1$.
Nguồn: Sưu tầm
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
