Câu 47 đề thi thử 2021 chuyên Trần Phú Hải Phòng
- 10/03/2021
- 67 lượt xem

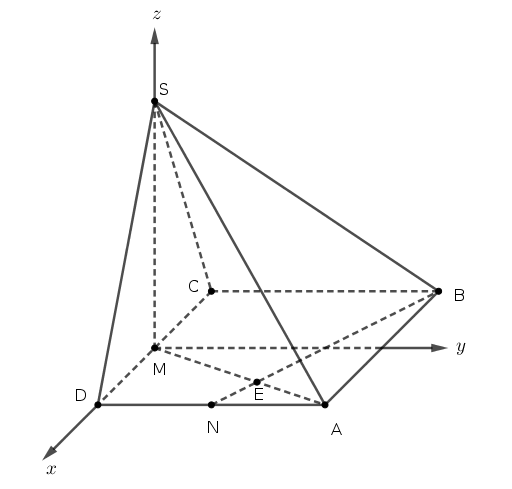
Phương pháp truyền thống: (dành cho HS giỏi HHKG)
Vì trục đường tròn ngoại tiếp tam giác CME (cũng chính là đường tròn đường kính BM) song song với $SM$ nên bán kính mặt cầu ngoại tiếp tứ diên $SCME$ xác định bởi công thức $$R=\sqrt{\dfrac{SM^2}{4}+\left(R_{(CME)}\right)^2}=\sqrt{\dfrac{SM^2}{4}+\dfrac{BC^2+CM^2}{4}}$$
Phương pháp tọa độ: (dành cho HS yêu thích PPTĐ)
Trong không gian chọn hệ trục tọa độ $Oxyz$ như hình vẽ và chon $a=1$đvd. Khi đó ta thấy ngay tọa độ của các điểm như sau: $$S\left(0;0;\dfrac{\sqrt3}{2}\right) ; M(0;0;0), C\left(-\dfrac12;0;0\right)$$
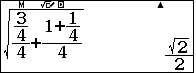
Trong mặt phẳng $ABCD$ chọn hệ trục tọa độ $Mxy$ như hình vẽ, khi đó $A(\dfrac12;1), M(0;0), B\left(-\dfrac12;1\right), N\left(\dfrac12;\dfrac12\right)$. Khi đó tọa độ giao điểm $E$ của $AM$ và $BN$ là:
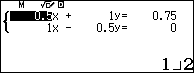

 , cao độ của $E$ bằng $0$.
, cao độ của $E$ bằng $0$.
Nhập hệ phương trình xác định mặt cầu 
kết quả  lần lượt lưu vào A, B, C.
lần lượt lưu vào A, B, C.
Do đó $R=\sqrt{a^2+b^2+c^2}=$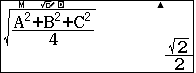
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
