BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Câu 43 Chuyên Vinh 2020 lần 2 (19/7/2020)
- 31/07/2020
- 97 lượt xem
Giải:
Áp dụng công thức (xem chứng minh trong bài trước)
| $$d(SD,BM)=\dfrac{12V_{SDBM}}{\sqrt{4c^2f^2-(a^2+d^2-b^2-e^2)^2}}$$ |
trong đó
- $c=SD=$
; $f=BM=$
- $a=SB=$
; $d=DM=$
- $b=SM=\sqrt{SA^2-AO^2+OM^2}=$
($O$ là tâm hình vuông); $e=BD=$
- Kết quả:
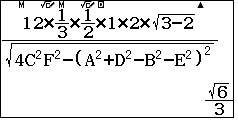chọn C.
Chia sẻ
About TS. Nguyễn Thái Sơn
