Ứng dụng xử lý số thập phân vô hạn tuần hoàn bằng Casio fx 580vnx

Thông thường khi ta nhập một phân số tối giản, kết quả có thể là một số thập phân vô hạn tuần hoàn.

Ví dụ: 

Kết quả ta được một số thập phân vô hạn tuần hoàn, phần tuần hoàn có 16 chữ số. Trong trường hợp số thập phân vô hạn tuần hoàn mà phần tuần hoàn có quá nhiều chữ số, máy tính có khả năng không xuất ra được kết quả là một số thập phân vô hạn tuần hoàn. Khi đó ta có thể can thiệp như ví dụ sau đây:

Ví dụ Chuyển phân số $ \large \frac{1}{109} $ thành số thập phân vô hạn tuần hoàn.

• w3 1Jz(A) Lưu tử số vào A. 
• A O10000000P 109 : A O 10000000 p 109 OMJ(A), sau đó nhấn dấu = 91743.

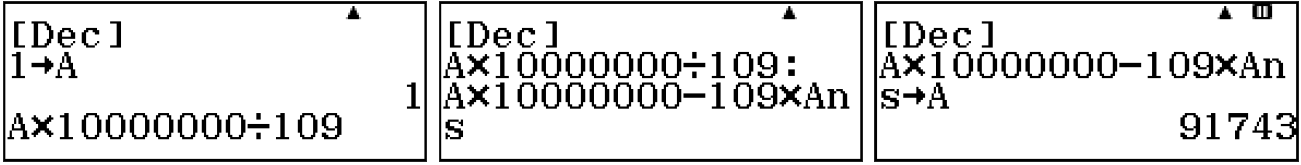
Vậy: $latex \large \dfrac{1}{109}=0,0091743 $

• Nhấn tiếp dấu = bỏ, nhấn tiếp dấu = 1192660 (lấy)

Lặp lại (bỏ/lấy) cho đến khi hết phần tuần hoàn, bắt đầu phần tuần hoàn là chữ số thứ 7 từ phải sang.

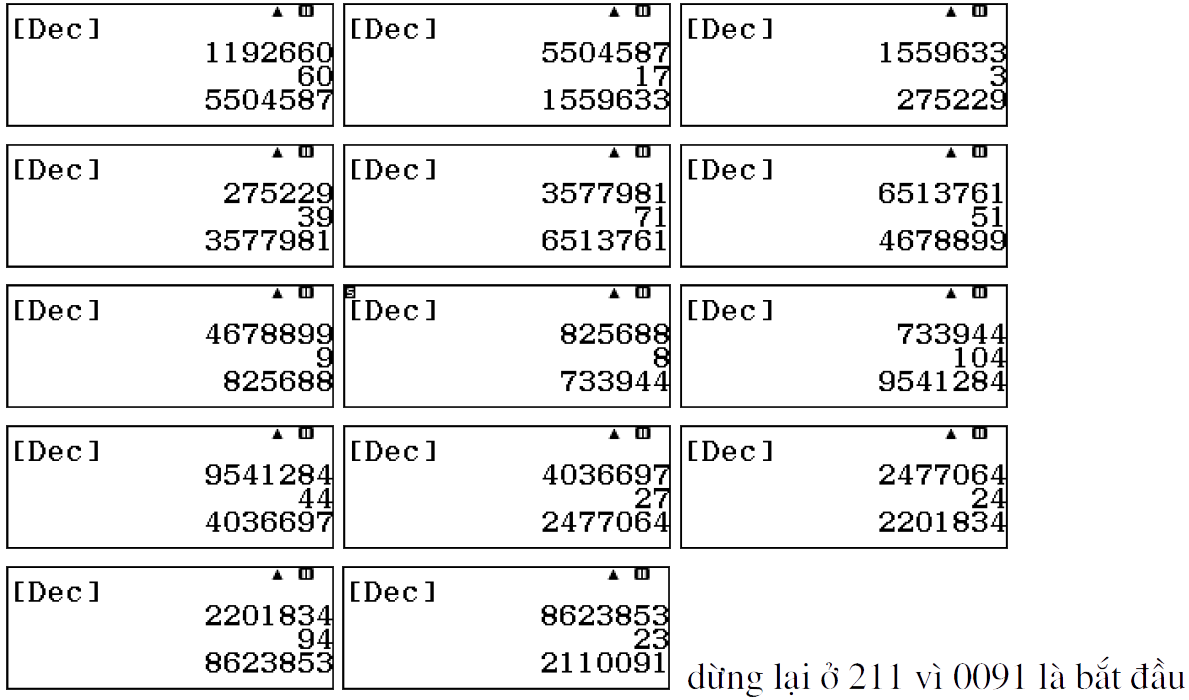
Ta có:

$latex \large \dfrac{1}{109}=0.(0091743119266055045871559633027522935779816513\\ \large761467889
90825688073394495412844036697247706422018348623853211)$

Giải thích:

1. Bài toán trên có ý nghĩa về mặt thuật toán, trong thực tế ta thường không gặp.
2. Sở dĩ nhân cho $latex \large 10000000=10^7 $ để mỗi lần chia ra thương, phần thương sẽ có 7 chữ số (nhanh hết lặp), nếu nhân cho $latex 10^8 $ thuật toán bị dừng đột ngột.
3. Sở dĩ dùng hệ thập phân w3 mà không dùng w1 để phép chia chỉ xuất ra thương, không xuất ra phần thập phân.
4. Phần sau dấu hai chấm là phần dư. Lấy số bị chia trừ đi tích của thương với số chia rồi đem lưu vào số bị chia mới có công dụng lặp.