BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Về công thức xác định góc giữa hai mặt bên của một khối tứ diện
- 05/08/2020
- 492 lượt xem
Đặt vấn đề: Cho khối tứ diện $ABCD$. Gọi $\varphi$ là góc tạo bởi hai mặt phẳng $(ACD)$ và $(BCD)$
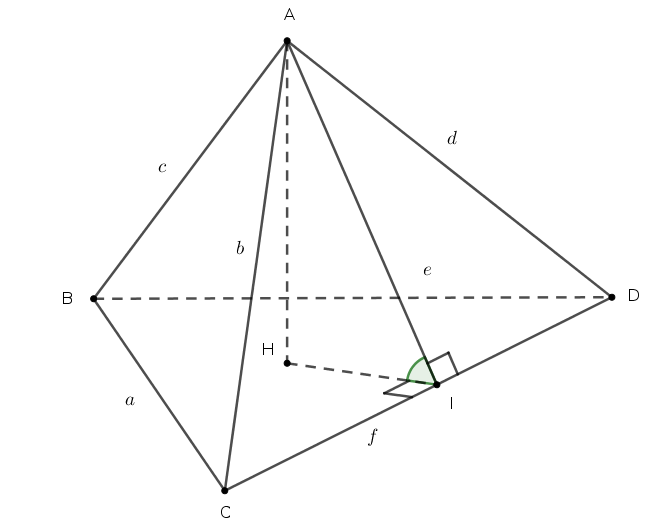
Ta có công thức
| $$\sin\varphi=\dfrac{3}{2}.\dfrac{V_{ABCD}.CD}{S_{ACD}.S_{BCD}}$$ |
Chứng minh: Hạ đường cao $AH$ của hình chóp. Hạ $HI \perp CD$. Khi đó góc $\widehat{AIH}$ là góc tạo bởi hai mặt phẳng $(ACD)$ và $(BCD)$. Trong tam giác vuông $AHI$ ta có: $$\sin\varphi=\dfrac{AH}{AI}=\dfrac{\dfrac{3V_{ABCD}}{S_{BCD}}}{\dfrac{2S_{ACD}}{CD}}=\dfrac{3}{2}.\dfrac{V_{ABCD}.CD}{S_{ACD}.S_{BCD}}$$
Áp dụng: Đề thi thử Chuyên Vinh lần 1 /2020
Giải:
Áp dụng công thức trên ta có:
$$\sin60^\circ=\dfrac32.\dfrac{V_{SABC}.AB}{S_{ABC}.S_{SAB}}\Rightarrow S_{SAB}=\dfrac32.\dfrac{V_{SABC}.AB}{S_{ABC}.\sin 60^\circ}=\dfrac{3V_{SABC}}{AC\sin 60^\circ}$$
Ta tính được:
$$d(I,(SAB))=\dfrac{3V_{SABI}}{S_{SAB}}=\dfrac{\dfrac32 V_{SABC}}{S_{SAB}}=\dfrac{\dfrac32 V_{SABC}}{\dfrac{3V_{SABC}}{AC\sin 60^\circ}}=\dfrac{AC.\sin 60^\circ}{2}=\dfrac{a\sqrt3}{4}$$
ta chọn A.
Nhận xét: Kết quả của bài toán không phụ thuộc vào hình chiếu vuông góc của $S$ trên mặt phẳng $(ABC)$, nghĩa là đã cho giả thiết góc giữa hai mặt phẳng $(SAB)$ và $(SAC)$ thì không cho thêm giả thiết hình chiếu vuông góc của $S$ trên mặt phẳng $(ABC)$. |
About TS. Nguyễn Thái Sơn
