BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Vấn đề tìm nguyên hàm của hàm số vô tỷ
- 04/09/2019
- 484 lượt xem
Do đặc thù của kỳ thi THPT QG là thi bằng hình thức trắc nghiệm, nên việc tính cho được nguyên hàm của một hàm số ngày càng mai một, ngay cả đối với người dạy. Hậu quả là nhiều sinh viên ĐH Bách khoa (rất cần giỏi tính toán) đã không vượt qua được yêu cầu đào tạo dù điểm số trúng tuyển đại học không phải thấp.
Trong bối cảnh đó, diễn đàn muốn trao đổi với một số thầy cô dạy Toán 12 về một chuỗi các tích phân rất thú vị nếu chúng ta đầu tư thời gian và công sức để tính được các tích phân đó.
Đặt vấn đề
Ta bắt đầu từ việc đơn giản nhất đó là tính $\int{\dfrac{1}{1+x}dx}$ và ta biết ngay $$\int{\dfrac{1}{1+x}dx}=\ln\left| x+1 \right|+C$$
Thêm một bước ta có
$$\int{\dfrac{1}{1+{{x}^{2}}}dx=\arctan x+C}$$
Vậy $\int{\dfrac{1}{1+{{x}^{3}}}dx}$ sẽ ra sao?
Trước khi bắt đầu công việc chúng ta cần biết công thức sau đây:
$$\int{\dfrac{dx}{a{{x}^{2}}+bx+c}}=\dfrac{2}{\sqrt{-\Delta }}\arctan \dfrac{2ax+b}{\sqrt{-\Delta }}+C$$
Trong đó $\Delta ={{b}^{2}}-4ac<0$.
Ta có: $\dfrac{1}{1+{{x}^{3}}}=\dfrac{A}{x+1}+\dfrac{Bx+C}{{{x}^{2}}-x+1}$
Bằng phương pháp hệ số bất định, giải hệ ba phương trình tuyến tính
Kết quả:
Vậy $$\dfrac{1}{1+x^{3}}=\dfrac{1}{3}\left[\dfrac{1}{1+x}-\dfrac{x-2}{x^{2}-x+1}\right]=\dfrac{1}{3}\left[\dfrac{1}{1+x}-\dfrac{1}{2} \cdot \dfrac{2 x-1-3}{x^{2}-x+1}\right]$$
Do đó
$$\int{\dfrac{1}{1+{{x}^{3}}}dx=\dfrac{1}{3}\ln \left| x+1 \right|-\dfrac{1}{6}\ln \left| {{x}^{2}}-x+1 \right|+\dfrac{1}{\sqrt{3}}\arctan \dfrac{2x-1}{\sqrt{3}}+C}$$
Kiểm tra trên máy tính Casio fx-580VNX
Mở w8 nhập hàm số
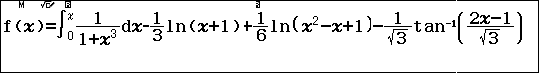
Cho $x$ chạy
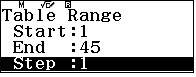
Kết quả là
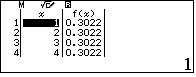
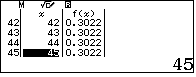
$45$ giá trị của $x$ đều cho kết quả là hằng $C=0.302299894$
Kết luận
$$\int{\dfrac{1}{1+{{x}^{3}}}dx=\dfrac{1}{3}\ln \left| x+1 \right|-\dfrac{1}{6}\ln \left| {{x}^{2}}-x+1 \right|+\dfrac{1}{\sqrt{3}}\arctan \dfrac{2x-1}{\sqrt{3}}+C}$$
Áp dụng cho câu trắc nghiệm:
Câu 1. Cho $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right)=\dfrac{1}{1+{{x}^{3}}}$ sao cho $F\left( 0 \right)=-\dfrac{\pi \sqrt{3}}{18}$. Khi đó $F\left( 1 \right)$ bằng
|
a. $\dfrac{1}{3}\ln 2-\dfrac{\pi \sqrt{3}}{18}$. b. $\dfrac{1}{3}\ln 3-\dfrac{\pi \sqrt{3}}{18}$ |
c. $\dfrac{1}{3}\ln 2+\dfrac{\pi \sqrt{3}}{18}$ d. $\dfrac{1}{3}\ln 2+\dfrac{\pi \sqrt{3}}{18}$ |
Hướng dẫn
Sử dụng máy tính Casio fx-580VNX
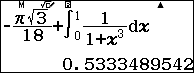
Thử phương án C
Lưu ý. Lời giải tự luận dành cho giáo viên dùng để ra đề, cách trả lời trên máy tính dành cho học sinh.
| Bài toán kì tới. Tìm nguyên hàm của hàm số $f\left( x \right)=\dfrac{1}{1+{{x}^{4}}}$. |
Diễn đàn thân mời các bạn tham gia viết lời giải tự luận cho nguyên hàm nói trên.
TS. Nguyễn Thái Sơn – Vũ Nhân Khánh
About Bitex Khánh Vũ
