BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Ứng dụng công thức tìm nguyên hàm của hàm số căn bậc hai của tanx
- 27/09/2019
- 2,852 lượt xem
Ở những bài viết trước, diễn đàn đã chia sẻ về cách tính những tích phân của các hàm số vô tỉ $\int{\dfrac{1}{1+{{x}^{n}}}dx}$ với $n=1,n=2,n=3$ và $n=4$.
Tiếp theo loạt bài viết này, chúng tôi trình bày cách tính nguyên hàm của hàm số $y=\sqrt{\tan x}$. Những bài tập này tuy không giúp ích được nhiều trong kì thi Trung học phổ thông quốc gia. Tuy nhiên nó sẽ giúp các bạn rèn luyện nhiều về kĩ năng tính toán và biến đổi. Một thứ khá cần thiết cho những ai đang muốn học những ngành liên quan đến kĩ thuật.
Tìm nguyên hàm của hàm số $y=\sqrt{\tan x}$
Trước khi đi vào tính toán, ta nhắc lại công thức sau:
$$\int{\dfrac{dx}{a{{x}^{2}}+bx+c}=\dfrac{2}{\sqrt{-\Delta }}\arctan \dfrac{2ax+b}{\sqrt{-\Delta }}+C}$$
Trong đó $\Delta ={{b}^{2}}-4ac<0$.
Đặt $t=\sqrt{\tan x}\Rightarrow x=\arctan {{t}^{2}}\Rightarrow dx=\dfrac{2tdt}{1+{{t}^{4}}}$.
Khi đó $\displaystyle I=\int{\sqrt{\tan x}dx\Rightarrow \int{\dfrac{2{{t}^{2}}dt}{1+{{t}^{4}}}}}$
Ta có: $\dfrac{2{{t}^{2}}}{1+{{t}^{4}}}=\dfrac{At+B}{{{t}^{2}}+\sqrt{2}t+1}+\dfrac{Ct+D}{{{t}^{2}}-\sqrt{2}t+1}$
Bằng phương pháp hệ số bất định, giải hệ bốn phương trình tuyến tính
$$\left\{ \begin{aligned} & A+C=0 \\ & -A\sqrt{2}+B+C\sqrt{2}+D=2 \\ & A-B\sqrt{2}+C+D\sqrt{2}=0 \\ & B+D=0 \\\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & A=-\dfrac{\sqrt{2}}{2} \\ & B=0 \\ & C=\dfrac{\sqrt{2}}{2} \\ & D=0 \\\end{aligned} \right.$$
Kết quả
Lưu hai nghiệm $x$ vào $A$ và $y$ vào $B$
Vậy $\dfrac{1}{1+{{t}^{4}}}=-\dfrac{\sqrt{2}}{4}\left[ \dfrac{2t+\sqrt{2}-\sqrt{2}}{{{t}^{2}}+\sqrt{2}t+1}-\dfrac{2t-\sqrt{2}+\sqrt{2}}{{{t}^{2}}-\sqrt{2}t+1} \right]$
Suy ra:
$$\int{\dfrac{2{{t}^{2}}dt}{1+{{t}^{4}}}=\dfrac{\sqrt{2}}{4}\ln \left| \dfrac{{{t}^{2}}-\sqrt{2}t+1}{{{t}^{2}}+\sqrt{2}t+1} \right|}+\dfrac{\sqrt{2}}{2}\arctan \dfrac{2t+\sqrt{2}}{\sqrt{2}}+\dfrac{\sqrt{2}}{2}\arctan \dfrac{2t-\sqrt{2}}{\sqrt{2}}+C$$
Do đó
$$\int{\dfrac{2{{t}^{2}}dt}{1+{{t}^{4}}}=\dfrac{\sqrt{2}}{4}\ln \left| \dfrac{{{t}^{2}}-\sqrt{2}t+1}{{{t}^{2}}+\sqrt{2}t+1} \right|}+\dfrac{\sqrt{2}}{2}\arctan \left( \sqrt{2}t+1 \right)+\dfrac{\sqrt{2}}{2}\arctan \left( \sqrt{2}t-1 \right)+C$$
Kiểm tra trên máy tính Casio fx-580VNX
Mở w8 nhập hàm số
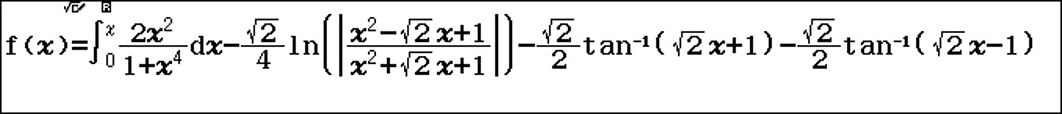
Cho $x$ chạy
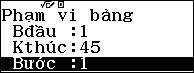
Kết quả là
$45$ giá trị của $x$ đều cho kết quả là hằng $C\approx 0$.
Kết luận$$\int{\sqrt{\tan x}dx=\dfrac{\sqrt{2}}{4}\ln \left| \dfrac{{{t}^{2}}-\sqrt{2}t+1}{{{t}^{2}}+\sqrt{2}t+1} \right|}+\dfrac{\sqrt{2}}{2}\arctan \left( \sqrt{2}t+1 \right)+\dfrac{\sqrt{2}}{2}\arctan \left( \sqrt{2}t-1 \right)+C$$
trong đó $t=\sqrt{\tan x}$.
Đây đã là phần tính toán cuối cùng trong bài viết. Tuy nhiên, nhằm muốn các Ở bài viết sau, diễn đàn sẽ chia sẻ đến mọi người một số công cụ tính toán trên máy tính nhằm giúp các bạn có thể thuận tiện hơn khi tính toán và kiểm tra những phép tính phức tạp. Trân trọng.
TS. Nguyễn Thái Sơn – Vũ Nhân Khánh
About Bitex Khánh Vũ
