BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
TÌM NHANH TIỆM CẬN CỦA HÀM SỐ TRÊN MÁY TÍNH CASIO FX 580VNX
- 31/08/2018
- 13,421 lượt xem
Bài toán tìm tiệm cận hàm số là một nội dung quan trọng trong chương I – Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số, chương trình Giải tích lớp 12. Nội dung này thường xuyên có mặt trong các đề thi, kiểm tra. Nắm được phương pháp xác định tiệm cận hàm số trên máy tính cầm tay CASIO fx 580VNX là mục tiêu của bài viết này.
Bài toán tìm tiệm cận hàm số sau: Số tiệm cận đứng của đồ thị hàm số [latex]\frac{\sqrt{x+9}-3}{{{x}^{2}}+x}[/latex]
là:
(Trích câu 18 – Mã đề 101 đề thi THPTQG 2018) |
Lời giải tự luận
Ta nhắc lại về định nghĩa tiệm cận đứng, đường thẳng $latex x={{x}_{0}}$ được gọi là đường tiệm cận đứng của đồ thị hàm số $latex y=f(x)$ nếu ít nhất một trong các điều kiện sau được thoả mãn:
$latex \underset{x\to x_{0}^{-}}{\mathop{\lim }}\,f(x)=+\infty \\ \underset{x\to x_{0}^{-}}{\mathop{\lim }}\,f(x)=-\infty \\ \underset{x\to x_{0}^{+}}{\mathop{\lim }}\,f(x)=+\infty \\ \underset{x\to x_{0}^{+}}{\mathop{\lim }}\,f(x)=-\infty$
Quay trở lại bài toán trên, ta có tập xác định của $latex f(x)$ là: $latex D=[-9;+\infty )\backslash \{0;1\}$.
Ta có: $latex \underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,\dfrac{\sqrt{x+9}-3}{{{x}^{2}}+x}=+\infty$ nên $latex x=-1$ là tiệm cận đứng
Mặc khác:
$latex \begin{align} & \underset{x\to 0}{\mathop{\lim }}\,\dfrac{\sqrt{x+9}-3}{{{x}^{2}}+x} \\ & =\underset{x\to 0}{\mathop{\lim }}\,\dfrac{\left( \sqrt{x+9}-3 \right)\left( \sqrt{x+9}+3 \right)}{\left( {{x}^{2}}+x \right)\left( \sqrt{x+9}+3 \right)} \\ & =\underset{x\to 0}{\mathop{\lim }}\,\dfrac{x+9-9}{\left( {{x}^{2}}+x \right)\left( \sqrt{x+9}+3 \right)} \\ & =\underset{x\to 0}{\mathop{\lim }}\,\dfrac{1}{\left( x+1 \right)\left( \sqrt{x+9}+3 \right)} \\ & =\dfrac{1}{6} \\ \end{align}$
Nên $latex x=0$ không phải là tiệm cận đứng.
Vậy chỉ có 1 đường tiệm cận đứng do đó ta chọn đáp án D.
Chúng ta có thể xác định nhanh giới hạn của $latex f(x)$ bằng máy tính cầm tay CASIO fx 580VNX như sau:
Bước 1: Nhập biểu thức $latex f(x)$
- Cách bấm: as[+9$p3R[d+[
- Máy tính hiển thị:
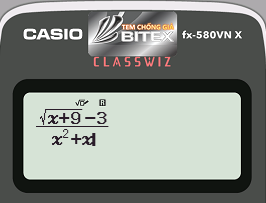
Bước 2: Để tính $latex \underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,\frac{\sqrt{x+9}-3}{{{x}^{2}}+x}$ ta có thể CALC tại giá trị $latex x=-1+{{10}^{-6}}\approx -1$
- Cách bấm: as[+9$p3R[d+[==
- Máy tính hiển thị:
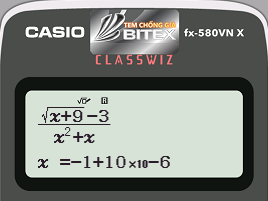
Từ kết quả ta dự đoán $latex \underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,\dfrac{\sqrt{x+9}-3}{{{x}^{2}}+x}=+\infty$ nên $latex x=-1$ là một tiệm cận đứng.
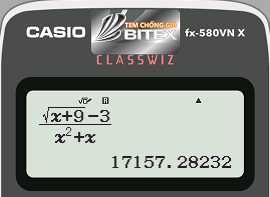
Bước 3: Để tính $latex \underset{x\to 0}{\mathop{\lim }}\,\dfrac{\sqrt{x+9}-3}{{{x}^{2}}+x}$ ta có thể CALC tại giá trị $latex x=0+{{10}^{-6}}\approx 0$
- Cách bấm: !r0+10Kp6==
- Máy tính hiển thị:
Từ kết quả ta dự đoán $latex \underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,\dfrac{\sqrt{x+9}-3}{{{x}^{2}}+x}=0,1666649544\approx \dfrac{1}{6}$ nên $latex x=0$ không là một tiệm cận đứng.
Các bạn tham khảo đồ thị của hàm số và đường tiệm cận đứng qua hình sau:
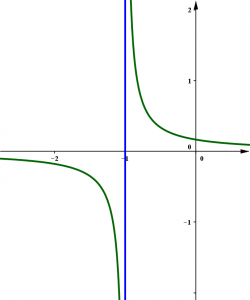
Trên đây diendanmaytinhcamtay.vn đã giới thiệu cho các bạn cách tìm tiệm cận đứng để giải bài toán tìm tiệm cận hàm số trong đề thi THPTQG 2018. Truy cập diễn đàn mỗi ngày để xem thêm nhiều bài toán ứng dụng hay về cách sử dụng máy tính cầm tay CASIO fx 580VNX.
About Bitex Casio
