BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
PHẦN 5: GIẢI QUYẾT NHỮNG BÀI TOÁN LUỸ THỪA MA TRẬN BẰNG PHƯƠNG THỨC MATRIX
- 25/01/2019
- 16,741 lượt xem
Trong loạt bài viết này ad đưa ra những hướng dẫn cơ bản nhất để có thể làm quen với phương thức Matrix. Từ đó ứng dụng nó để giải quyết những bài toán Đại số tuyến tính từ đơn giản đến phức tạp. Ngoài ra, loạt bài viết này còn ứng dụng phương thức ma trận để giải quyết một số bài toán trắc nghiệm ở chương trình trung học phổ thông. Phần 5 này ad sẽ sử dụng phương thức matrix trên cả 2 loại máy tính để làm cái mà nó làm tốt nhất: giải quyết những bài toán về ma trận luỹ thừa.
Trong loạt bài viết này ad đưa ra những hướng dẫn cơ bản nhất để có thể làm quen với phương thức Matrix (ma trận). Từ đó ứng dụng nó để giải quyết những bài toán Đại số tuyến tính từ đơn giản đến phức tạp. Ngoài ra, loạt bài viết này còn ứng dụng phương thức ma trận để giải quyết một số bài toán trắc nghiệm ở chương trình trung học phổ thông. Phần 5 này ad sẽ sử dụng phương thức matrix trên cả 2 loại máy tính để làm cái mà nó làm tốt nhất: giải quyết những bài toán về ma trận luỹ thừa.
IV. Sử dụng phương thức matrix để giải quyết một số bài toán về ma trận luỹ thừa
1. Giải quyết một số bài toán ma trận luỹ thừa căn bản
Ở đây ad sẽ chia sẻ đến mọi người hai bài toán ma trận luỹ thừa căn bản thường gặp
Bài toán ma trận 1:
Cho ma trận $latex A=\left( \begin{matrix} 13 & -1 & 5 \\ 0 & 7 & -6 \\ 8 & -1 & 6 \\\end{matrix} \right)$ và ma trận $latex B=\left( \begin{matrix} -7 & 19 & -15 \\ 20 & -13 & 14 \\ -12 & 19 & -14 \\\end{matrix} \right)$
Tìm ma trận $latex X$ sao cho $latex X-A+B=20{{I}_{3}}$, trong đó $latex {{I}_{3}}$ là ma trận đơn vị cấp 3.
Hướng dẫn
*Trên máy tính Casio fx-570VN Plus
Nhập 3 ma trận A,B,I vô máy tính
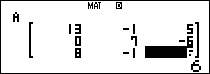
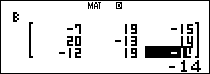
Thực hiện phép tính $latex X=A-B+20{{I}_{3}}$
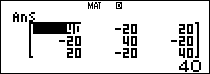
Vậy $latex X=\left( \begin{matrix} 40 & -20 & 20 \\ -20 & 40 & -20 \\ 20 & 20 & 40 \\\end{matrix} \right)$.
*Trên máy tính Casio fx-580VN X
Nhập 2 ma trận A,B vô máy tính
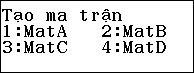
Thực hiện phép tính $latex X=A-B+20{{I}_{3}}$
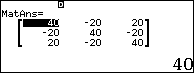
Vậy $latex X=\left( \begin{matrix} 40 & -20 & 20 \\ -20 & 40 & -20 \\ 20 & 20 & 40 \\\end{matrix} \right)$.
Bài toán ma trận 2:
Cho ma trận $latex A=\left[ \begin{matrix} 0 & 1 & -1 \\ -2 & 1 & 0 \\ 3 & 0 & 1 \\\end{matrix} \right]$. Tính $latex {{A}^{2}}+{{A}^{T}}-5{{I}_{3}}$, trong đó $latex {{I}_{3}}$ là ma trận đơn vị cấp 3.
Hướng dẫn
*Trên máy tính Casio fx-570VN Plus
Nhập 2 ma trận $latex A,I$ vào máy tính
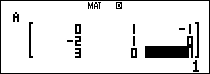
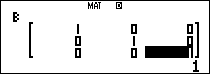
Tính $latex {{A}^{2}}$
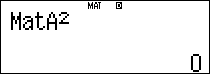
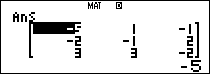
Tính $latex {{A}^{2}}+{{A}^{T}}-5{{I}_{3}}$
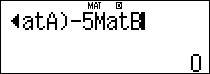
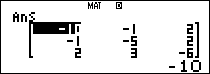
Vậy $latex {{A}^{2}}+{{A}^{T}}-5I=\left[ \begin{matrix} -10 & -1 & 2 \\ -1 & -5 & 2 \\ 2 & 3 & -6 \\\end{matrix} \right]$.
*Trên máy tính Casio fx-580VN X
Nhập ma trận $latex A$vào máy tính
Tính $latex {{A}^{2}}$
Tính $latex {{A}^{2}}+{{A}^{T}}-5{{I}_{3}}$
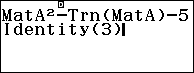
Vậy $latex {{A}^{2}}+{{A}^{T}}-5I=\left[ \begin{matrix} -10 & -1 & 2 \\ -1 & -5 & 2 \\ 2 & 3 & -6 \\\end{matrix} \right]$.
2. Giải quyết một số bài toán luỹ thừa phức tạp bằng phương pháp quy nạp
Bài toán ma trận 3:
Cho $latex A=\left( \begin{matrix} 0 & 1 \\ -1 & 0 \\\end{matrix} \right)$, hãy tính $latex {{A}^{2000}}$
Hướng dẫn
*Trên máy tính Casio fx-570VN Plus
Nhập ma trận $latex A$ vào máy tính
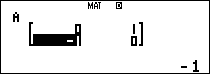
Ta tìm một số ma trận luỹ thừa của $latex A$
$latex {{A}^{2}}$:
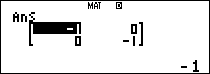
$latex {{A}^{3}}$: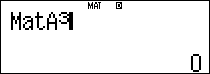
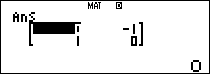
$latex {{A}^{4}}$: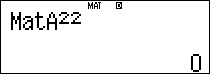
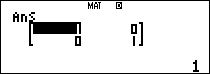
Mà $latex 2000\vdots 4$
Vậy $latex {{A}^{2000}}={{\left( {{A}^{4}} \right)}^{500}}={{\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\\end{matrix} \right)}^{500}}=\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\\end{matrix} \right)={{I}_{2}}$.
*Trên máy tính Casio fx-580VN X
Nhập ma trận $latex A$ vào máy tính
Ta tìm một số ma trận luỹ thừa của $latex A$
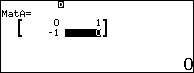
$latex {{A}^{2}}$:
$latex {{A}^{3}}$:
$latex {{A}^{4}}$:
Mà $latex 2000\vdots 4$
Vậy $latex {{A}^{2000}}={{\left( {{A}^{4}} \right)}^{500}}={{\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\\end{matrix} \right)}^{500}}=\left( \begin{matrix} 1 & 0 \\ 0 & 1 \\\end{matrix} \right)={{I}_{2}}$.
Bài toán ma trận 4:
Cho ma trận $latex A=\left[ \begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\\end{matrix} \right]$. Hãy tính $latex {{A}^{n}}$.
Hướng dẫn
* Giải trên máy tính Casio fx-570VN Plus
Nhập ma trận vào máy tính
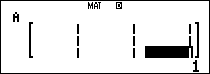
Ta tính thử một số số hạng đầu của ma trận
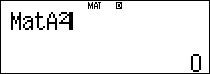
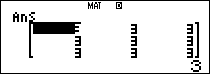
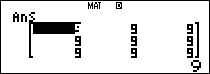
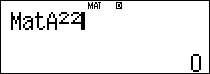
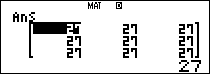
Vậy ta có thể dự đoán công thức chung của ma trận như sau
$latex {{A}^{n}}=\left( \begin{matrix} {{3}^{n-1}} & {{3}^{n-1}} & {{3}^{n-1}} \\ {{3}^{n-1}} & {{3}^{n-1}} & {{3}^{n-1}} \\ {{3}^{n-1}} & {{3}^{n-1}} & {{3}^{n-1}} \\\end{matrix} \right)$
Ta chứng minh quy nạp cho công thức $latex {{A}^{n}}=\left( \begin{matrix} {{3}^{n-1}} & {{3}^{n-1}} & {{3}^{n-1}} \\ {{3}^{n-1}} & {{3}^{n-1}} & {{3}^{n-1}} \\ {{3}^{n-1}} & {{3}^{n-1}} & {{3}^{n-1}} \\\end{matrix} \right)$
Ta có $latex {{A}^{1}}=\left( \begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\\end{matrix} \right)=\left( \begin{matrix} {{3}^{0}} & {{3}^{0}} & {{3}^{0}} \\ {{3}^{0}} & {{3}^{0}} & {{3}^{0}} \\ {{3}^{0}} & {{3}^{0}} & {{3}^{0}} \\\end{matrix} \right)=\left( \begin{matrix} {{3}^{1-1}} & {{3}^{1-1}} & {{3}^{1-1}} \\ {{3}^{1-1}} & {{3}^{1-1}} & {{3}^{1-1}} \\ {{3}^{1-1}} & {{3}^{1-1}} & {{3}^{1-1}} \\\end{matrix} \right)$ (đúng)
Ta giả sử công thức đúng với $latex n=k$:
$latex {{A}^{k}}=\left( \begin{matrix} {{3}^{k-1}} & {{3}^{k-1}} & {{3}^{k-1}} \\ {{3}^{k-1}} & {{3}^{k-1}} & {{3}^{k-1}} \\ {{3}^{k-1}} & {{3}^{k-1}} & {{3}^{k-1}} \\\end{matrix} \right)$.
Ta chứng minh công thức đúng với $latex n=k+1$:
$latex {{A}^{k+1}}={{A}^{k}}.A=\left( \begin{matrix} {{3}^{k-1}} & {{3}^{k-1}} & {{3}^{k-1}} \\ {{3}^{k-1}} & {{3}^{k-1}} & {{3}^{k-1}} \\ {{3}^{k-1}} & {{3}^{k-1}} & {{3}^{k-1}} \\\end{matrix} \right)\left( \begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\\end{matrix} \right)=\left( \begin{matrix} {{3}^{k}} & {{3}^{k}} & {{3}^{k}} \\ {{3}^{k}} & {{3}^{k}} & {{3}^{k}} \\ {{3}^{k}} & {{3}^{k}} & {{3}^{k}} \\\end{matrix} \right)$
$latex \Rightarrow $ Đpcm.
[dropshadowbox align=”none” effect=”lifted-both” width=”auto” height=”” background_color=”#ffffff” border_width=”1″ border_color=”#dddddd” ]Lời bình. Ở một số dạng toán luỹ thừa bậc cao, chúng ta nên sử dụng máy tính để tính toán trước những bậc mũ nhỏ. Từ đó, ta có thể dự đoán công thức chung của ma trận mũ đó rồi chứng minh quy nạp hoặc tính trực tiếp như câu số 3 để ra được kết quả.[/dropshadowbox]Bài toán ma trận 5:
Tính ma trận $latex {{A}^{2017}}$ trong đó
$latex A=\left( \begin{matrix} 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\\end{matrix} \right)$
Hướng dẫn
* Trên máy tính Casio fx-580VNX
Nhập ma trận vào máy tính
Ta tính thử một số luỹ thừa đầu
Ta dự đoán kết quả chính xác $latex {{A}^{n}}=\left( \begin{matrix} {{2}^{n-1}} & 0 & 0 & {{2}^{n-1}} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ {{2}^{n-1}} & 0 & 0 & {{2}^{n-1}} \\\end{matrix} \right)$.
Chứng minh qui nạp kết quả ta suy ra $latex {{A}^{2017}}=\left( \begin{matrix} {{2}^{2016}} & 0 & 0 & {{2}^{2016}} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ {{2}^{2016}} & 0 & 0 & {{2}^{2016}} \\\end{matrix} \right)$
———————————————
Trên đây là một số hướng dẫn giải những bài toán ma trận luỹ thừa trên 2 dòng máy tính thịnh hành nhất hiện nay là Casio fx-570VN Plus và Casio fx-580 VNX, Bài viết còn nhiều thiếu sót (dù đã được chỉn chu), các bạn có góp ý, bình luận đừng ngại gửi tin nhắn hoặc bình luận trên fanpage nhá. Thanks for attention.
Đón xem phần 6: PHẦN 6: GIẢI QUYẾT NHỮNG BÀI TOÁN LUỸ THỪA MA TRẬN BẰNG PHƯƠNG THỨC MATRIX (II)
Bài viết trước: PHẦN 4: SỬ DỤNG PHƯƠNG THỨC MA TRẬN TRÊN MÁY TÍNH CASIO ĐỂ GIẢI NHỮNG BÀI TOÁN THPT
About Bitex Khánh Vũ
