BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
MỘT SỐ CÔNG THỨC GIẢI NHANH BÀI TOÁN ĐIỂM CỰC TRỊ HÀM SỐ TRÙNG PHƯƠNG
- 12/09/2018
- 9,596 lượt xem
Chúng ta thường gặp các dạng câu hỏi “Tìm $latex M$ để đồ thị hàm trùng phương có ba điểm cực trị hàm số thỏa mãn một tính chất”. Việc trang bị cho mình các công thức giải nhanh từ đó vận dụng máy tính cầm tay CASIO fx 580VNX ta có thể giải quyết nhanh các dạng toán này. Trong bài viết này diendanmaytinhcamtay.vn sẽ cung cấp cho các bạn các công thức giải nhanh thường gặp, mời các bạn theo dõi.
Để giải dạng toán xác định cực trị hàm số ta thường đi qua 2 bước:
Bước 1: Tìm điều kiện để hàm số có ba cực trị $latex (ab<0)$
Bước 2: Gọi $latex A({{x}_{A}};{{y}_{A}}),B({{x}_{B}};{{y}_{B}});C({{x}_{C}};{{y}_{C}})$ là tọa độ các điểm cực trị hàm số trong đó $latex A\in Oy$. Ta có tọa độ 3 điểm cực trị như sau:
$latex A(0;c),B\left( -\sqrt{-\dfrac{b}{2a}};\dfrac{{{b}^{2}}-4ac}{4a} \right),C\left( \sqrt{-\dfrac{b}{2a}};\dfrac{{{b}^{2}}-4ac}{4a} \right)$
Do hàm số trùng phương nhận trục tung làm trục đối xứng nên tam giác $latex ABC$ luôn cân tại $latex A$ do đó ta có bảng tổng hợp các tính chất thường gặp như sau:
|
Tính chất/Yêu cầu |
Công thức giải nhanh |
Khi $latex a=1$ |
| Tính góc $latex \widehat{BAC}=\alpha $ | $latex {{\cot }^{2}}\dfrac{\alpha }{2}=\dfrac{-{{b}^{3}}}{8a}$ | $latex {{\cot }^{2}}\dfrac{\alpha }{2}=\dfrac{-{{b}^{3}}}{8}$ |
| Tam giác $latex ABC$ vuông cân (tại A) | $latex {{b}^{3}}=-8a$ | $latex b=-2$ |
| Tam giác $latex ABC$ đều | $latex {{b}^{3}}=-24a$ | $latex b=-2\sqrt[3]{3}$ |
| Tính diện tích tam giác $latex ABC$ | $latex S=\left| a \right|{{\left( \sqrt{-\dfrac{b}{2a}} \right)}^{5}}$ | $latex S={{\left( \sqrt{-\dfrac{b}{2}} \right)}^{5}}$ |
| Tính bán kính đường tròn nội tiếp tam giác $latex ABC$ | $latex r=\dfrac{{{b}^{2}}}{4\left| a \right|\left( 1+\sqrt{1-\frac{{{b}^{3}}}{8a}} \right)}$ | $latex r=\dfrac{{{b}^{2}}}{4\left( 1+\sqrt{1-\frac{{{b}^{3}}}{8}} \right)}$ |
| Tính bán kính đường tròn ngoại tiếp tam giác $latex ABC$ | $latex R=\dfrac{{{b}^{3}}-8a}{8\left| a \right|b}$ | $latex R=\dfrac{{{b}^{3}}-8}{8b}$ |
Diendanmaytinhcamtay.vn khuyến khích các bạn hiểu bản chất của từng công thức, không nên học thuộc lòng một cách máy móc các công thức cực trị hàm số này. Cách học hiệu quả nhất là vận dụng qua các bài tập về cực trị hàm số. Dưới đây diendanmaytinhcamtay.vn sẽ trình bày cách chứng minh các công thức trên:
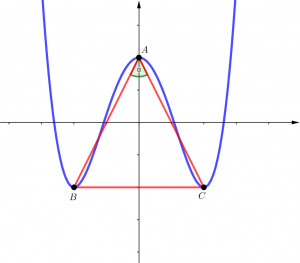
- Đặt $latex \widehat{BAC}=\alpha $ và gọi $latex I$ là giao điểm của $latex BC$ và $latex Oy$, ta có:
- Tính góc $latex \widehat{BAC}=\alpha $: $latex \cot \dfrac{\alpha }{2}=\frac{AI}{BI}=\dfrac{\left| -\dfrac{{{b}^{2}}-4ac}{4a}-c \right|}{\sqrt{-\dfrac{b}{2a}}}=\dfrac{b}{2}\sqrt{-\dfrac{b}{2a}}\Rightarrow {{\cot }^{2}}\dfrac{\alpha }{2}=\dfrac{-{{b}^{3}}}{8a}$
- Tam giác $latex ABC$ vuông cân tại $latex A$ $latex \Rightarrow \alpha ={{90}^{o}}\Rightarrow \dfrac{b}{2}\sqrt{-\dfrac{b}{2a}}=1\Rightarrow {{b}^{3}}=-8a$
- Tam giác $latex ABC$ đều (vì $latex ABC$ cân nên chỉ cần thêm điều kiện $latex \alpha ={{60}^{o}}$)$\Rightarrow \dfrac{b}{2}\sqrt{-\dfrac{b}{2a}}=\sqrt{3}\Rightarrow {{b}^{3}}=-24a$
- Tính diện tích tam giác $latex ABC$: $latex S=\dfrac{1}{2}BC.AI=\sqrt{-\dfrac{b}{2a}}.\left| -\dfrac{{{b}^{2}}-4ac}{4a}-c \right|=\sqrt{-\dfrac{{{b}^{5}}}{32{{a}^{3}}}}=\left| a \right|{{\left( \sqrt{-\dfrac{b}{2a}} \right)}^{5}}$
- Tính bán kính đường tròn nội tiếp tam giác $latex ABC$: $latex r=\dfrac{S}{p}=\dfrac{S}{2AB+BC}=\dfrac{\left| a \right|{{\left( \sqrt{-\dfrac{b}{2a}} \right)}^{5}}}{2\sqrt{\dfrac{{{b}^{4}}}{16{{a}^{2}}}-\dfrac{b}{2a}}+2\sqrt{-\dfrac{b}{2a}}}\Rightarrow r=\dfrac{{{b}^{2}}}{4\left| a \right|\left( 1+\sqrt{1-\dfrac{{{b}^{3}}}{8a}} \right)}$
- Tính bán kính đường tròn ngoại tiếp tam giác $latex ABC$: $latex R=\dfrac{AB.AC.BC}{4S}=\dfrac{A{{B}^{2}}.BC}{4S}=\dfrac{\left( \dfrac{{{b}^{4}}}{16{{a}^{2}}}-\dfrac{b}{2a} \right).2\sqrt{-\dfrac{b}{2a}}}{4\left| a \right|{{\left( \sqrt{-\dfrac{b}{2a}} \right)}^{5}}}\Rightarrow R=\dfrac{{{b}^{3}}-8a}{8\left| a \right|b}$
Hi vọng với các công thức giải nhanh này các bạn sẽ vận dụng để giải quyết các bài toán trắc nghiệm về cực trị hàm số tiết kiệm thời gian hơn. Các ví dụ vận dụng những công thức giải nhanh trên sẽ được diendanmaytinhcamtay.vn trình bày trong các bài viết tiếp theo.
About Bitex Casio
