Ba cách tính khoảng cách giữa hai đường thẳng chéo nhau (3)

Sử dụng công thức

$$d(AB,CD)=\dfrac{12V_{ABCD}}{\sqrt{4.AB^2.CD^2-\left(AC^2+BD^2-AD^2-BC^2\right)^2}}$$

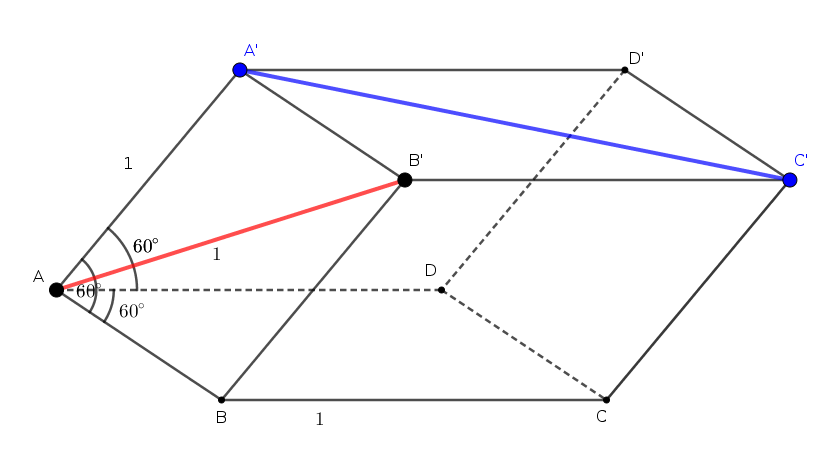
Tính $d(AB’,A’C’)$. Xét tứ diện $AB’A’C’$, ba cặp cạnh đối như sau:

• $\bullet \quad AB’=\sqrt3$ vì $\widehat{AA’B’}=120^\circ, A’A=A’B’=1$
• $\quad A’C’=AC=\sqrt3$ (như trên)
• $\bullet \quad AA’=1$
• $\ \quad B’C’=1$
  $A’C^2=A’H^2+HC^2=AA’^2-HA^2+HC^2\Rightarrow A’C=\sqrt2$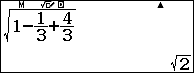 (H như trong hình vẽ của cách 2)
  Suy ra $AC’$ được tính như sau: $$AC’^2+A’C^2=2(AC^2+AA’^2)$$
  (trong một hình bình hành tổng bình phương của hai đường chéo thì bằng tổng bình phương của 4 cạnh)
• $\bullet \quad AC’=\sqrt6$
• $ \quad A’B’=1$

Thể tích khối tứ diện khi biết 6 cạnh được tính như sau:

$$V_{AB’A’C’}=\dfrac{1}{12}\sqrt{9(-6+2+7)+1(6-2+7)+6(6+2-7)-(3+18+18+3 )}=\dfrac{\sqrt2}{12}$$

(Xem công thức tính thể tích khối tứ diện khi biết 6 cạnh trên diễn đàn này)

Suy ra $d(AB’,A’C’)=\dfrac{12V}{\sqrt{4AB’^2.A’C’^2-(AA’^2+B’C’^2-AC’^2-A’B’^2)^2}}$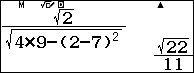

Nhận xét: Cách này cũng tính toán phiền toái, tuy nhiên có một ưu điểm là nếu tìm được độ dài 6 cạnh của khối tứ diện thì chỉ cần thay số vào công thức. Muốn học cách tính toán nhanh với công thức chúng tôi sẽ trình bày sau.

About TS. Nguyễn Thái Sơn

nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). Giảng viên thỉnh giảng ĐHSP TP HCM.