Ba cách tính khoảng cách giữa hai đường thẳng chéo nhau (2)

Sử dụng PPTĐ trong không gian.

Nhận xét rằng nếu một hình lăng trụ, hoặc hình chóp mà có đáy là tam giác đều ta dễ dàng dùng PPTĐ như sau:

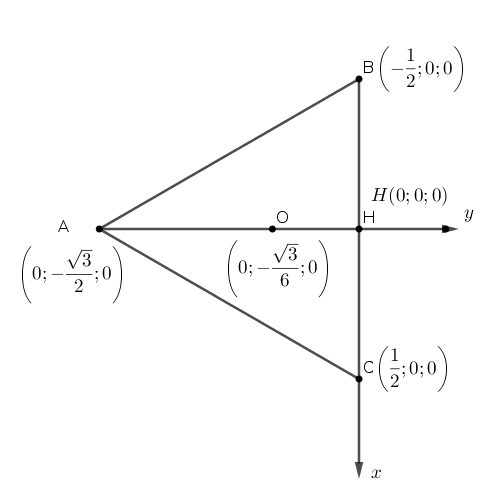
Chọn trung điểm $H$ của $BC$ làm gốc tọa độ, chọn cạnh của tam giác đều làm 1 đvd, hướng của các tia theo qui tắc tam diện thuận. Trục $z$ đi qua $H$ và vuông góc với mặt phẳng $(ABC)$.

Ví dụ: Cho một hình hộp $ABCDA’B’C’D’$ có tất cả các cạnh đều bằng $1$ và các góc phẳng đỉnh $A$ đều bằng $60^\circ$. Tính $d(AB’, A’C’)$.

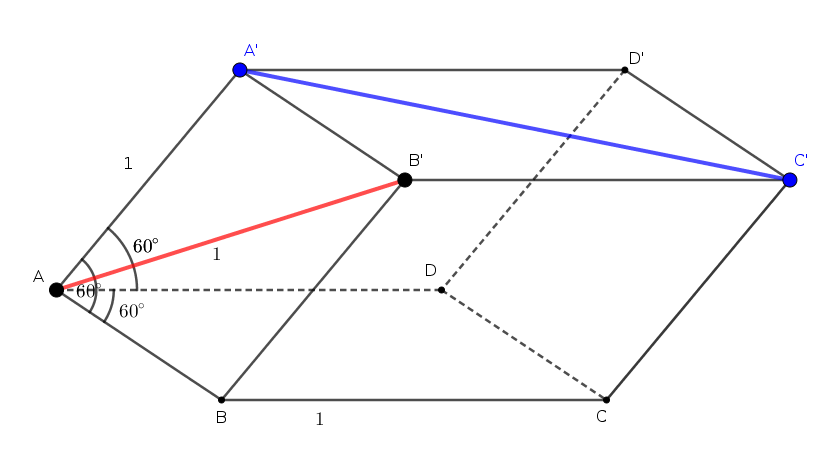
Giải:

Chọn hệ trục tọa độ như hình vẽ:

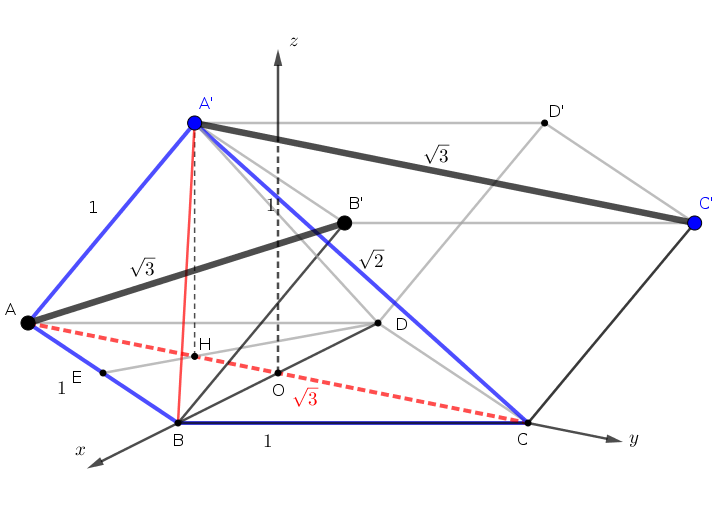
$$A\left(0;-\dfrac{\sqrt3}{2};0\right), B\left(\dfrac12;0;0\right), A’\left(0;-\dfrac{\sqrt3}{6};\dfrac{\sqrt6}{3}\right)$$

Chú ý: $AC=\sqrt3, AH=\dfrac13AC \Rightarrow A’H=\sqrt{1-\dfrac13}=\dfrac{\sqrt6}{3}$.

Vì $\overrightarrow{A’B’}=\overrightarrow{AB} \Rightarrow B’\left\{\begin{array}{l} x=x_B-x_A+x_{A’}=\dfrac12 \\ y=y_B-y_A+y_{A’}=\dfrac{\sqrt3}{3}\\ z=z_B-z_A+z_{A’}=\dfrac{\sqrt6}{3}\end{array}\right.$

Xét ba vectơ $$\overrightarrow{AB’}=\left(\dfrac12;\dfrac{5\sqrt3}{6};\dfrac{\sqrt6}{3}\right); \overrightarrow{A’C’}=\overrightarrow{AC}=2\overrightarrow{AO}=\left(0;\sqrt3;0\right); \overrightarrow{AA’}=\left(0;\dfrac{\sqrt3}{3};\dfrac{\sqrt6}{3}\right)$$

Vậy $d(AB’,A’C’)=\dfrac{\sqrt{22}}{11}$

Nhận xét: Phương pháp này cũng tính toán phiền toái nhưng định hướng rõ ràng, dễ cho học sinh thực hiện và đặc biệt là tính được trực tiếp khoảng cách giữa hai đường thẳng  chéo nhau không cần thông qua bước dựng hình.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013).