BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
KIỂM TRA SỰ LIÊN TỤC CỦA HÀM SỐ DƯỚI SỰ HỖ TRỢ CỦA CASIO FX 580 VNX
- 17/02/2019
- 2,339 lượt xem
Các bài toán về sự liên tục của hàm số thường xuất hiện trong các đề thi, kiểm tra và gây nhiều khó khăn cho học sinh. Trong bài viết này, chúng tôi sẽ trình bày một dạng toán khá phổ biến , đó là cách xác định tham số m để hàm số đã cho liên tục tại một điểm dưới sự hỗ trợ của máy tính Casio fx– 580 VNX thông qua 2 bài toán cụ thể sau:
Cho hàm số $latex y=f\left( x \right)$ xác định trên tập $latex D$ và $latex {{x}_{0}}\in D$. Khi đó $latex y=f\left( x \right)$ được gọi là liên tục tại $latex {{x}_{0}}$ nếu $latex \underset{x\to {{x}_{0}}}{\mathop{\lim }}\,f\left( x \right)=f\left( {{x}_{0}} \right)$
Bài toán 1. Tìm tham số $latex m$ để hàm số liên tục trên $latex \mathbb{R}$ với $latex f\left( x \right)=\left\{ \begin{align} & \dfrac{6-x-{{x}^{2}}}{x-2},x\ne 2 \\ & -2x-m,x=2 \\\end{align} \right.$
- $latex m=1$
- $latex m=4$
- $latex m=2$
- $latex m=0$
Hướng dẫn giải
Hàm số $latex f\left( x \right)$ liên tục trên $latex \mathbb{R}$ khi và chỉ khi
$ \dfrac{{{\left. \dfrac{d\left( 6-x-{{x}^{2}} \right)}{dx} \right|}_{x=2}}}{{{\left. \dfrac{d\left( x-2 \right)}{dx} \right|}_{x=2}}}={{\left. \left( -2x-m \right) \right|}_{x=2}}$ $latex \Leftrightarrow \dfrac{{{\left. \dfrac{d\left( 6-x-{{x}^{2}} \right)}{dx} \right|}_{x=2}}}{{{\left. \dfrac{d\left( x-2 \right)}{dx} \right|}_{x=2}}}=-4-m$ $latex \Leftrightarrow m=-\dfrac{{{\left. \dfrac{d\left( 6-x-{{x}^{2}} \right)}{dx} \right|}_{x=2}}}{{{\left. \dfrac{d\left( x-2 \right)}{dx} \right|}_{x=2}}}-4$
Sử dụng máy tính Casio fx 580vnx để tìm m:
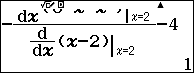
Chọn đáp án A
Tổng quát:
[dropshadowbox align=”none” effect=”lifted-both” width=”auto” height=”” background_color=”#ffffff” border_width=”1″ border_color=”#dddddd” ]Hàm số $latex f\left( x \right)=\left\{ \begin{align} & g\left( x \right),x={{x}_{0}} \\ & \dfrac{{{h}_{1}}\left( x \right)}{{{h}_{2}}\left( x \right)},x\ne {{x}_{0}} \\\end{align} \right.$ liên tục tại $latex {{x}_{0}}$ khi và chỉ khi $latex \left\{ \begin{align} & {{h}_{1}}\left( {{x}_{0}} \right)=0 \\ & \dfrac{{{h}_{1}}^{\prime }\left( {{x}_{0}} \right)}{{{h}_{2}}^{\prime }\left( {{x}_{0}} \right)}=g\left( {{x}_{0}} \right) \\\end{align} \right.$[/dropshadowbox]Bài toán 2. Cho hàm số $latex f\left( x \right)=\left\{ \begin{align} & \dfrac{4-{{x}^{2}}}{\sqrt{x+2}-2},x>2 \\& mx-20,x\le 2 \\\end{align} \right.$ . Tìm $latex m$ để hàm số liên tục tại $latex x=2$
- $latex m=1$
- $latex m=4$
- $latex m=2$
- $latex m=5$
Hướng dẫn giải
Hàm số $latex f\left( x \right)$ liên tục tại $latex x=2$ khi và chỉ khi
$latex \dfrac{{{\left. \dfrac{d\left( 4-{{x}^{2}} \right)}{dx} \right|}_{x=2}}}{{{\left. \dfrac{d\left( \sqrt{x+2}-2 \right)}{dx} \right|}_{x=2}}}={{\left. \left( mx-20 \right) \right|}_{x=2}}$ $latex \Leftrightarrow m=\dfrac{1}{2}\left( \dfrac{{{\left. \dfrac{d\left( 4-{{x}^{2}} \right)}{dx} \right|}_{x=2}}}{{{\left. \dfrac{d\left( \sqrt{x+2}-2 \right)}{dx} \right|}_{x=2}}}+20 \right)$
Sử dụng máy tính Casio fx 580 vnx để tìm m:
Chọn đáp án C
Tổng quát.
[dropshadowbox align=”none” effect=”lifted-both” width=”auto” height=”” background_color=”#ffffff” border_width=”1″ border_color=”#dddddd” ]Hàm số $latex f\left( x \right)=\left\{ \begin{align} & g\left( x \right),x\le {{x}_{0}} \\& \dfrac{{{h}_{1}}\left( x \right)}{{{h}_{2}}\left( x \right)},x>{{x}_{0}} \\\end{align} \right.$ liên tục tại $latex {{x}_{0}}$ khi và chỉ khi $latex \dfrac{{{h}_{1}}^{\prime }\left( {{x}_{0}} \right)}{{{h}_{2}}^{\prime }\left( {{x}_{0}} \right)}=g\left( {{x}_{0}} \right)$[/dropshadowbox]Cảm ơn các bạn đã theo dõi bài viết KIỂM TRA SỰ LIÊN TỤC CỦA HÀM SỐ DƯỚI SỰ HỖ TRỢ CỦA CASIO FX 580VNX . Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
About Ngọc Hiền Bitex
