BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI NHANH PHƯƠNG TRÌNH BẬC NHẤT SIN,COS TRÊN CASIO FX 580VNX
- 31/08/2018
- 9,151 lượt xem
Phương trình bậc nhất đối với sin và cos có dạng $latex a\sin x+b\cos x=c$. Đây là một phương trình thường gặp trong chương trình Toán lớp 11. Cuối bài viết diendanmaytinhcamtay.vn sẽ bật mí cho các bạn “thủ thuật” dùng máy tính CASIO fx 580VNX để giải nhanh phương trình này.
Bài toán: Giải các phương trình bậc nhất sin,cos sau:
|
Lời giải:
1.Giải phương trình bậc nhất sau $latex \sqrt{3}\sin x-\cos x=\sqrt{2}$, ta có:
$latex \begin{align} & \sqrt{3}\sin x-\cos x=\sqrt{2} \\ & \Leftrightarrow \frac{\sqrt{3}}{2}\sin x-\frac{1}{2}\cos x=\frac{\sqrt{2}}{2} \\ & \Leftrightarrow \cos \frac{\pi }{6}\sin x-\sin \frac{\pi }{6}\cos x=\sin \frac{\pi }{4} \\ & \Leftrightarrow \sin \left( x-\frac{\pi }{6} \right)=\sin \frac{\pi }{4} \\ \end{align}$
$latex \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{6}=\frac{\pi }{4}+k2\pi \\ & x-\frac{\pi }{6}=\pi -\frac{\pi }{4}+k2\pi \\ \end{align} \right.(k\in \mathbb{Z})$
$latex \Leftrightarrow \left[ \begin{align} & x=\frac{5\pi }{12}+k2\pi \\ & x=\frac{11\pi }{12}+k2\pi \\ \end{align} \right.(k\in \mathbb{Z})$
Vậy nghiệm của phương trình đã cho là: $latex \left[ \begin{align} & x=\frac{5\pi }{12}+k2\pi \\ & x=\frac{11\pi }{12}+k2\pi \\ \end{align} \right.(k\in \mathbb{Z})$
2. Giải phương trình bậc nhất sau $latex \cos 2x+\sin x=\sqrt{3}\left( \cos x-\sin 2x \right)$, ta có:
$latex \begin{align} & \cos 2x+\sin x=\sqrt{3}\left( \cos x-\sin 2x \right) \\ & \Leftrightarrow \cos 2x+\sqrt{3}\sin 2x=\sqrt{3}cox-\sin x \\ & \Leftrightarrow \frac{1}{2}\cos 2x+\frac{\sqrt{3}}{2}\sin 2x=\frac{\sqrt{3}}{2}cox – \frac{1}{2}\sin x \\ & \Leftrightarrow \sin \frac{\pi }{6}\cos 2x+\cos \frac{\pi }{6}\sin 2x=\sin \frac{\pi }{3}cox-\cos \frac{\pi }{3}\sin x \\ & \Leftrightarrow \sin \left( 2x+\frac{\pi }{6} \right)=\sin \left( \frac{\pi }{3}-x \right) \\ \end{align}$
$latex \Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{18}+\frac{k2\pi }{3} \\ & x=\frac{\pi }{2}+k2\pi \\ \end{align} \right.(k\in \mathbb{Z})$
Vậy nghiệm của phương trình đã cho là: $latex \left[ \begin{align} & x=\frac{\pi }{18}+\frac{k2\pi }{3} \\ & x=\frac{\pi }{2}+k2\pi \\ \end{align} \right.(k\in \mathbb{Z})$
Diendanmaytinhcamtay.vn xin hướng dẫn các bạn cách sử dụng máy tính cầm tay CASIO fx-580VNX để thực hiện biến đổi biểu thức sau:
$latex a\sin u+b\cos u=c\Leftrightarrow \sin (u+Y)=\dfrac{c}{X}$
Để thực hiện trên máy tính ta sẽ dùng tính năng $latex Pol(a,b)$ với $a,b$ là hệ số trên phương trình, khi đó các giá trị $latex X,Y$ sẽ được lưu trong biến $latex x$ và biến $latex y$ của máy.
Lấy ví dụ phương trình $latex \sqrt{3}\sin x-\cos x=\sqrt{2}$ ta sẽ biến đổi về dạng $latex \sin (x+Y)=\dfrac{\sqrt{2}}{X}$, để tìm $latex X$ và $latex Y$ ta thực hiện trên máy như sau:
Bước 1: Chuyển sang đơn vị góc Radian
Cách bấm: qw22
Bước 2: Nhập và tính biểu thức $latex Pol(\sqrt{3},-1)$ (với $latex a=\sqrt{3},b=-1$)
- Cách bấm: q+s3$q)1)=
- Máy tính hiển thị:
Bước 3: Xem kết quả biến $latex x$ và $latex y$
- Cách bấm: Q(=Q)=
- Máy tính hiển thị:
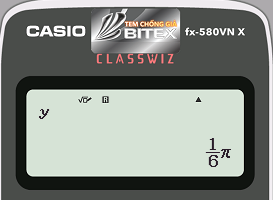
Vậy $latex \sqrt{3}\sin x-\cos x=\sqrt{2}\Leftrightarrow \sin \left( x+\dfrac{\pi }{6} \right)=\dfrac{\sqrt{2}}{2}$.
Hãy truy cập diendanmaytinhcamtay.vn để nhận được các bài viết hay mỗi ngày.
About Bitex Casio
