BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Tính đạo hàm cấp 2 trên máy tính Casio fx 580vnx
- 09/12/2018
- 5,240 lượt xem
Gần đây một số giáo viên có sáng kiến dùng máy tính cầm tay để tính gần đúng đạo hàm cấp hai. Đây là việc làm rất đáng khích lệ để khai thác khả năng tính toán của máy tính. Tuy nhiên chúng tôi cũng muốn lưu ý các bạn, là do bộ nhớ của máy tính cầm tay (calculator) có mức độ, do đó khả năng tính toán của nó không thể so sánh với các máy vi tính (computer). Vì thế thuật toán là đúng nhưng kết quả chỉ chấp nhận với sai số tương đối. Để đối sánh, chúng tôi dùng phần mềm máy tính và bộ vi xử lý của máy vi tính để tính toán song hành.
Ví dụ Tính đạo hàm cấp hai của hàm số cho ở dưới tại [latex]\large x=a=\frac{1}{6}[/latex] và để tính gần đúng với Casio fx 580vnx lấy số gia [latex]\large h=10^{-7}[/latex]
Cho hàm số [latex]\large f[/latex] với
[latex]\large f(x)=\frac{2.x^2+\ln(x)+1}{3.x^2-e^x+1}[/latex]
đạo hàm của [latex]\large f[/latex] theo biến [latex]\large x[/latex]:
[latex]\large f'(x)=\frac{2.x^3e^x-4.x^2e^x-6.x^2\ln(x)+x^2+xe^x\ln(x)+xe^x-e^x+1}{9.x^5-6.x^3e^x+6.x^3+x(e^x)^2-2.xe^x+x}[/latex]Đạo hàm cấp 2:
[latex]\large f”(x)=\frac{P(x)}{Q(x)}[/latex]
với:
[latex]\large Q(x)=27.x^8-27.x^6e^x+27.x^6+9.x^4(e^x)^2-18x^4e^x+9.x^4-x^2(e^x)^3+3.x^2(e^x)^2-3.x^2e^x+x^2[/latex][latex]\large P(x)=6.x^6e^x-24.x^5e^x+2.x^4(e^x)^2+3.x^4e^x\ln(x)+41.x^4e^x+54.x^4\ln(x)-27.x^4-8.x^3(e^x)^2[/latex] [latex]\large-24.x^3e^x\ln(x)-10.x^3e^x+x^2(e^x)^2\ln(x)+5.x^2(e^x)^2+7.x^2e^x\ln(x)+17.x^2e^x-6.x^2ln(x)[/latex] [latex]\large-20.x^2-2.x(e^x)^2+2.xe^x-(e^x)^2+2e^x-1[/latex]
Với:
[latex]\large a=\frac{1}{6},h=10^{-7}[/latex]
Biểu thức:
[latex]\large f'(a)=-81.9030967623[/latex]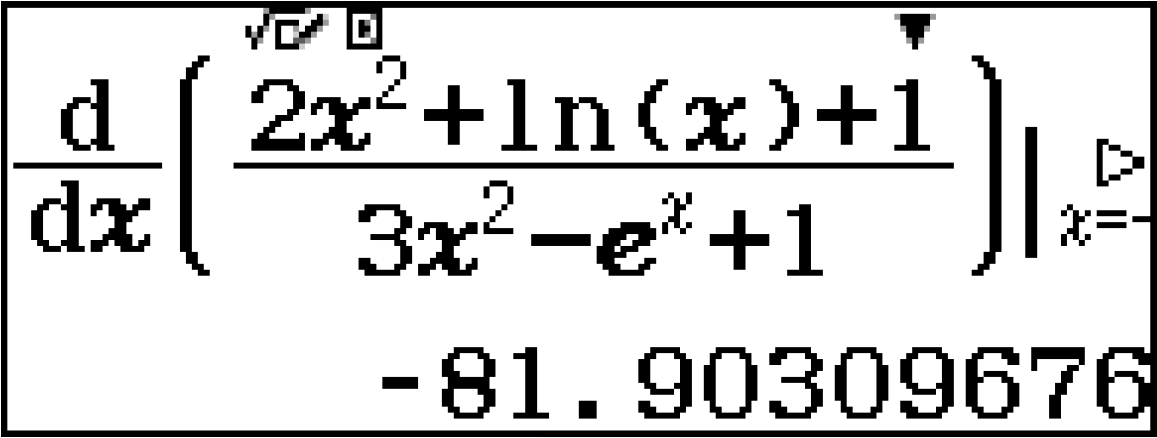
[latex]\large f'(a+h)=-81.9029968952[/latex] 
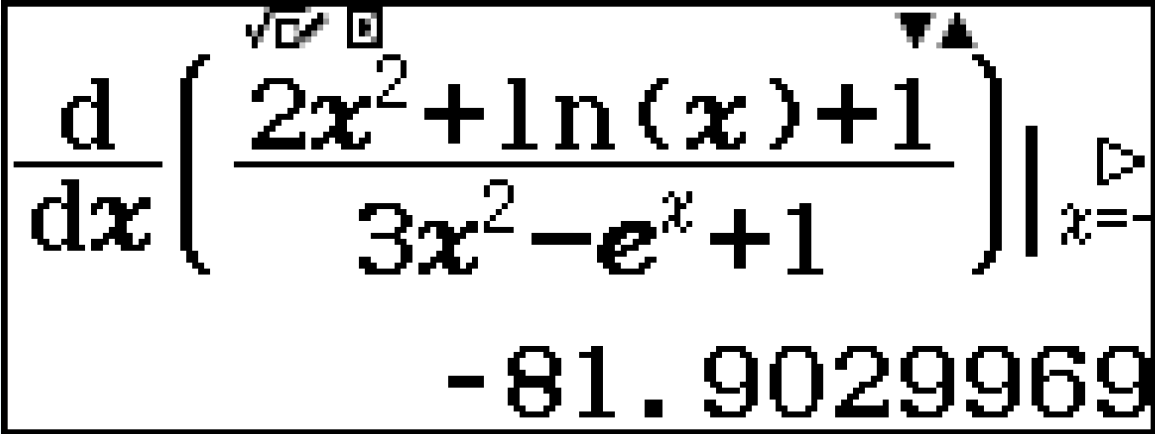[latex]\large \frac{f'(a+h)-f'(a)}{h}=998.671698653[/latex]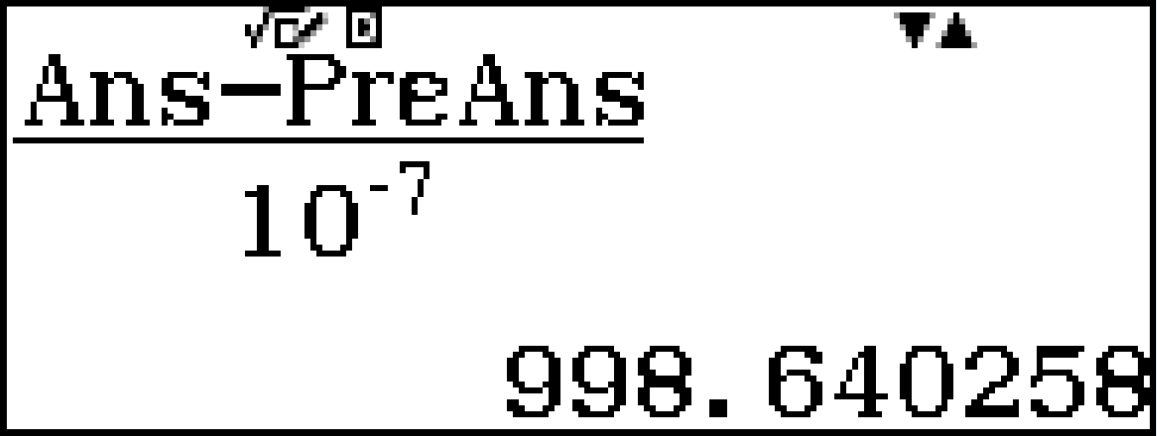 
Biểu thức chính xác:
[latex]\large f”(a) = 998.672536571[/latex]
Sai số: 0.0008
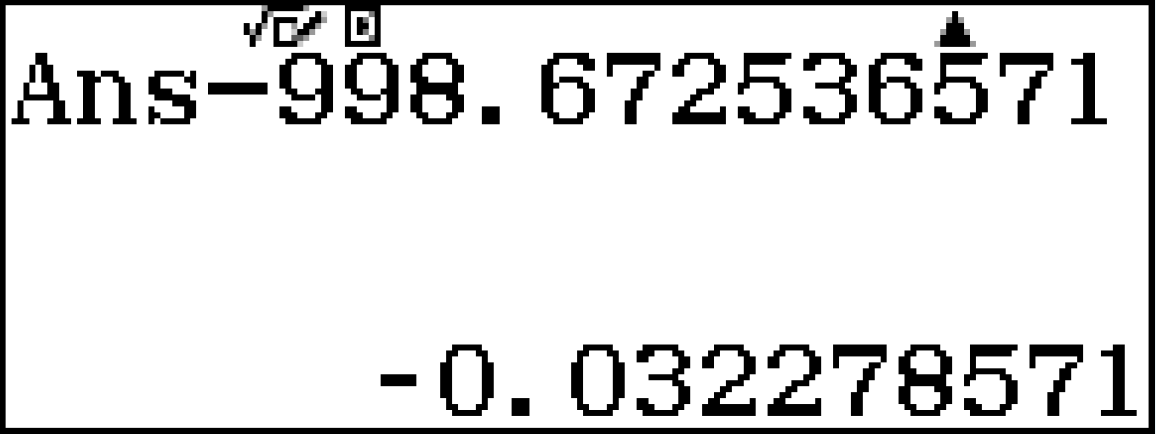
Phần nằm trong khung là so sánh với máy tính CASIO fx-580VN X. Tuy nhiên để trả lời câu trắc nghiệm thì sai số trên vẫn trong khả năng chấp nhận được. Cũng cần lưu ý với số gia [latex]\large 10^{-7}[/latex] kết quả tính được sẽ có sai số thấp nhất.
About Bitex_PTGD
