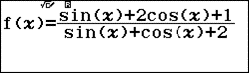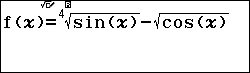SỬ DỤNG CASIO fx- 580VNX ĐỂ TÌM NHANH GTNN VÀ GTLN CỦA HÀM SỐ LƯỢNG GIÁC- PHẦN 2

Tìm GTLN và GTNN của một hàm số lượng giác là một dạng toán khó, thường khiến học sinh tốn rất nhiều thời gian và đòi hỏi khả năng kỹ thuật xử lý, biến đổi công thức lượng giác tốt khi giải bằng phương pháp tự luận truyền thống. Tiếp nối Phần 1, trong Phần 2 này Diễn đàn Toán Casio sẽ tiếp tục trình bày thêm một vài ví dụ về việc tìm nhanh GTLN và GTNN của hàm số lượng giác trên máy tính Casio fx 580VNX.

Bài toán 2. Giả sử $M$ và $m$ lần lượt là GTLN và GTNN của hàm số $y=\dfrac{\sin x+2\cos x+1}{\sin x+\cos x+2}$ trên $\mathbb{R}$. Tìm $M+m$ A. $1+\sqrt{2}$ B. $0$ C. $1$ D. $-1$ Hướng dẫn giải Chuyển máy tính về chế độ Radian qw22 Cài đặt tính toán phương thức TABLE với một hàm số qwRR11 Vào phương thức TABLE w8 Nhập vào hàm số $f\left( x \right)=\dfrac{\sin x+2\cos x+1}{\sin x+\cos x+2}$và bảng giá trị với $Start=0;End=2\pi ;Step=\dfrac{2\pi }{44}$

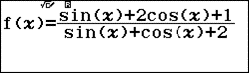
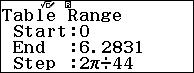
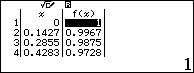
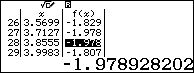
Dựa vào bảng giá trị ta có $M+m\approx -1$ Đáp án D Bài toán 3. Tìm GTLN và GTNN của hàm số $y=\sqrt[4]{\sin x}-\sqrt{\cos x}$ A. $\max y=1;\min y=-1$ B. $\max y=1;\min y=0$ C. $\max y=2;\min y=-1$ D. $\max y=2;\min y=0$ Hướng dẫn giải Phương pháp sử dụng máy tính Casio fx 580VNX Chuyển máy tính về chế độ Radian qw22 Cài đặt tính toán phương thức TABLE với một hàm số qwRR11 Vào phương thức TABLE w8 Nhập vào hàm số $f\left( x \right)=\sqrt[4]{\sin x}-\sqrt{\cos x}$ và bảng giá trị với $Start=0;End=\dfrac{\pi }{2};Step=\dfrac{\pi }{88}$

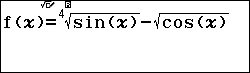
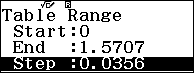
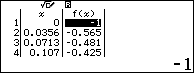
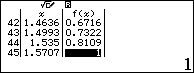
Dựa vào bảng giá trị ta có $\max y=1$ tại $x=\dfrac{\pi }{2}+k2\pi $ và $\min y=-1$ tại $x=k2\pi $ Đáp án A Phương pháp tự luận Hàm số $y=\sqrt[4]{\sin x}-\sqrt{\cos x}$ xác định khi và chỉ khi $\left\{ \begin{align}  & \sin x\ge 0 \\ & \cos x\ge 0 \\\end{align} \right.$ Ta có: $y=\sqrt[4]{\sin x}-\sqrt{\cos x}\le \sqrt[4]{\sin x}\le 1$ Suy ra $\max y=1$. Dấu bằng xảy ra khi và chỉ khi $\left\{ \begin{align}  & \cos x=0 \\ & \sin x=1 \\\end{align} \right.$ $\Leftrightarrow x=\dfrac{\pi }{2}+k2\pi $ Mặt khác ta có: \[y=\sqrt[4]{\sin x}-\sqrt{\cos x}\ge -\sqrt{\cos x}\ge -1\] Suy ra $\min y=-1$. Dấu bằng xảy ra khi và chỉ khi $\left\{ \begin{align}  & \cos x=1 \\ & \sin x=0 \\\end{align} \right.$ $\Leftrightarrow x=k2\pi $

---

Mọi ý kiến đóng góp và các câu hỏi thắc mắc về các bài viết hướng dẫn giải toán casio cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO