BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Bảng Hoocner - Bảng Taylor
- 24/10/2017
- 813 lượt xem
Chủ đề Bảng Hoocner - Bảng Taylor
Đề bài: Viết đa thức [latex]Q(x)=x^7-10x^6+36x^5-52x^4+16x^3+2005x^2-7957x+9964[/latex] dưới dạng lũy thừa của nhị thức bậc nhất [latex]x-2[/latex].
Lời giải:
Tìm các hệ số:
[latex]Q(x)=a_1 (x-2)^7+a_2 (x-2)^6 + a_3 (x-2)^5 + a_4 (x-2)^4 +a_5(x-2)^3 + a_6 (x-2)^2+a_7 (x-2)+a_8 [/latex].Công thức tổng quát cho dạng bài này:
Bước 1: Tìm [latex]a_8=P(2)=2006[/latex].
Tìm [latex]a_1[/latex]: Dễ thấy [latex]a_1=1[/latex].
Bước 2: Tìm [latex]a_7;\,a_2[/latex]:
+ [latex]a_7[/latex] tìm bằng cách tính giá trị biểu thức sau tại [latex]x=2[/latex].
Khi đó ta được đa thức:
[latex]\dfrac{P(x)-2006}{x-2}-a_1(x-2)^6-a_7=4x^5-40x^4+148x^3-248x^2+2181x-4042[/latex]Hệ số cao nhất của đa thức này (gọi là đa thức [latex]R(x)[/latex]): [latex]a_2=4[/latex].
Bước 3: Tính [latex]a_6;\, a_3[/latex]:
+ [latex]a_6[/latex] tìm bằng cách tính giá trị biểu thức sau tại [latex]x=2[/latex].
Khi đó ta được đa thức thức:
Thực hiện việc tính toán tương tự, ta được đa thức:
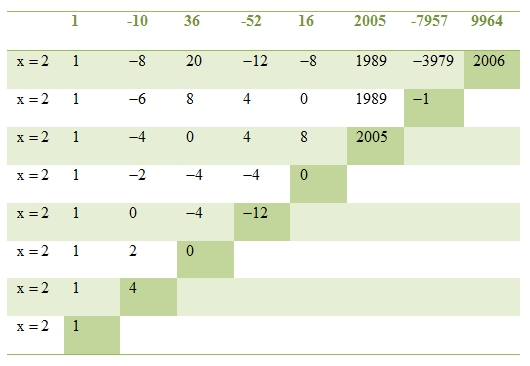
Cách 2: Dùng khai triển Taylor (Taylor expansion):
Định lý: Nếu hàm số [latex]y=f(x)[/latex] có các đạo hàm [latex]f’(x),\,f’’(x),\, …,\, f^{(n)}(x)[/latex] liên tục tại điểm [latex]x_0[/latex] và có đạo hàm [latex] f^{(n+1)}(x)[/latex] trong lân cận của [latex]x_0[/latex] thì tại lân cận đó ta có công thức khai triển:
[latex] \begin{array}{ccc} f(x) & = & f\left(x_{0}\right)+\dfrac{f’\left(x_{0}\right)}{1!}\left(x-x_{0}\right)+\dfrac{f”\left(x_{0}\right)}{2!}\left(x-x_{0}\right)^{2}+\,…\\ & & +\dfrac{f^{(n)}\left(x_{0}\right)}{n!}\left(x-x_{0}\right)^{n}+\dfrac{f^{(n+1)}(c)}{n!}\left(x-x_{0}\right)^{n+1} \end{array}[/latex]Với [latex]c\in \left(x_{0};\,x\right);\,c=x_{0}+a\left(x-x_{0}\right),\,0<a<1[/latex].
Với công này ta có thể giải nhanh bài toán trên. Với đạo hàm cấp 8 thì số hạng dư không còn nên ta không để ý tới số hạng dư này nữa.
Bước 1: Tìm [latex]a_{1}[/latex]:
[latex] a_{1}=\dfrac{f^{7}\left(x_{0}\right)}{7!}=\dfrac{7!}{7!}=1[/latex]Bước 2: Tìm [latex]a_{2}[/latex]:
[latex]a_{2}=\dfrac{f^{6}\left(x_{0}\right)}{6!}=\dfrac{\left[7!x-10.6!\right](2)}{6!}=4[/latex]Bước 3: Tìm [latex]a_{3}[/latex]:
[latex]a_{3}=\dfrac{f^{5}\left(x_{0}\right)}{5!}=\dfrac{\left[7.6.5.4.3x^{2}-10.6!x+36.5!\right](2)}{5!}=0[/latex]Bước 4: Tìm [latex]a_{4}[/latex]:
[latex] a_{4}=\dfrac{f^{4}\left(x_{0}\right)}{4!}=\dfrac{\left[7.6.5.4x^{3}-10.6.5.4.3.x^{2}+36.5!.x-52.4!\right](2)}{4!}=\dfrac{-288}{4!}=-12[/latex]Ta nhìn thấy ngay công thức Tổ hợp – chỉnh hợp
Bước 5: Tìm [latex]a_{5}[/latex]:
[latex] a_{5}=C_{7}^{4}.2^{4}-10.C_{6}^{3}.2^{3}+36.C_{5}^{2}.2^{2}-52C_{4}^{1}.2+16C_{3}^{0}=0[/latex]Bước 6: Tìm [latex]a_{6}[/latex]:
[latex]a_{6}=C_{7}^{5}.2^{5}-10.C_{6}^{4}.2^{4}+36.C_{5}^{3}.2^{3}-52C_{4}^{2}.2^{2}+16C_{3}^{1}.2+2005.C_{2}^{0}=2005[/latex]Bước 7: Tìm [latex]a_{7}[/latex]:
[latex] a_{7}=C_{7}^{6}.2^{6}-10.C_{6}^{5}.2^{5}+36.C_{5}^{4}.2^{4}-52C_{4}^{3}.2^{3}+16C_{3}^{2}.2^{2}+2005.C_{2}^{1}+C_{1}^{0}=-1[/latex]Bước 8: Tìm [latex]a_{8}[/latex]:
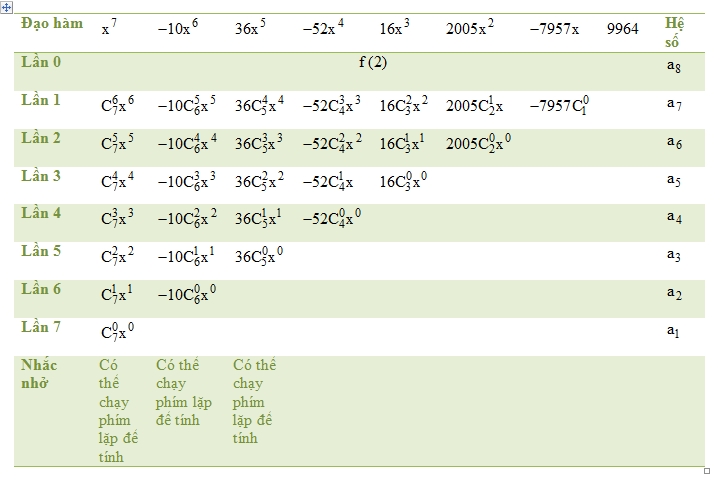
[latex]a_{8}=f(2)=2006[/latex].Ta cũng có bảng sau:
About TailieuCasio
