Áp dụng Ma Trận để giải hệ phương trình 4 ẩn trên máy tính Casio fx 580vnx

Ví dụ: Trong không gian $latex Oxyz$ cho bốn điểm

$latex A(1;-2;-1),B(-5;10;-1),C(4;1;11),D(-8;-2;2)$

Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ là:

A. $latex (-2;4;5)$         B. $latex (2;-4;-5)$          C. $latex (5;4;-2)$          D. $latex (-5;-4;2)$

Phương trình mặt cầu có dạng:

$latex x^2+y^2+z^2-2ax-2by-2cz+d=0$

Thay toạ độ của điểm nằm trên mặt cầu vào phương trình:

$latex -2ax_0-2by_0-2cz_0+d=-(x_0^2+y_0^2+z_0^2)$

Thay vì vào w914 để giải hệ phương trình tuyến tính bốn ẩn ta có thể sử dụng w4144 để nhập ma trận vuông cấp 4 và T1241 để nhập ma trận 4 dòng 1 cột như sau:

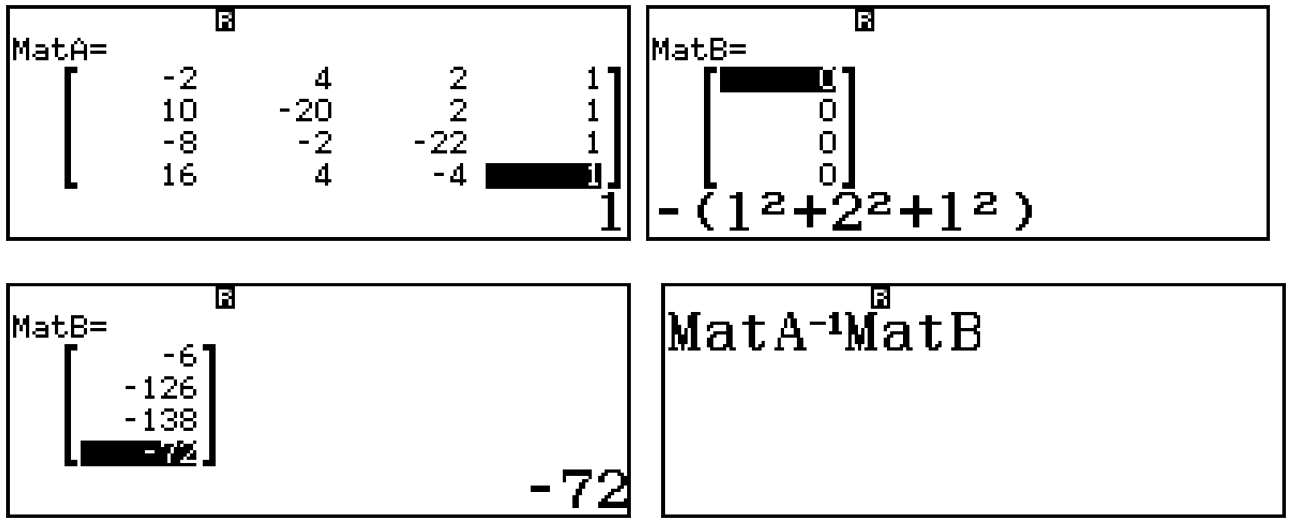
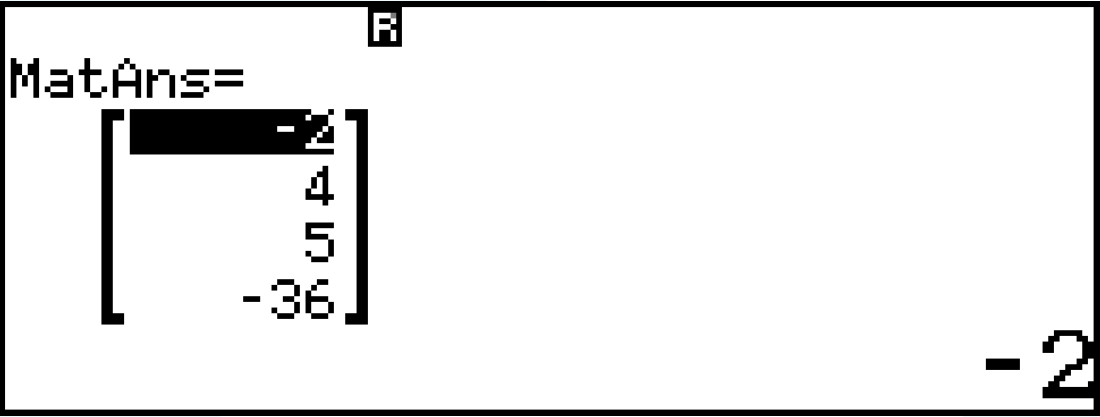
Như các bạn thấy, ta có tất cả thông tin của mặt này trên một màn hình. Cụ thể tâm của mặt cầu là $latex I (-2;-4;5)$

Giải thích. Một hệ phương trình tuyến tính 4 ẩn có thể viết dưới dạng ma trận như sau:

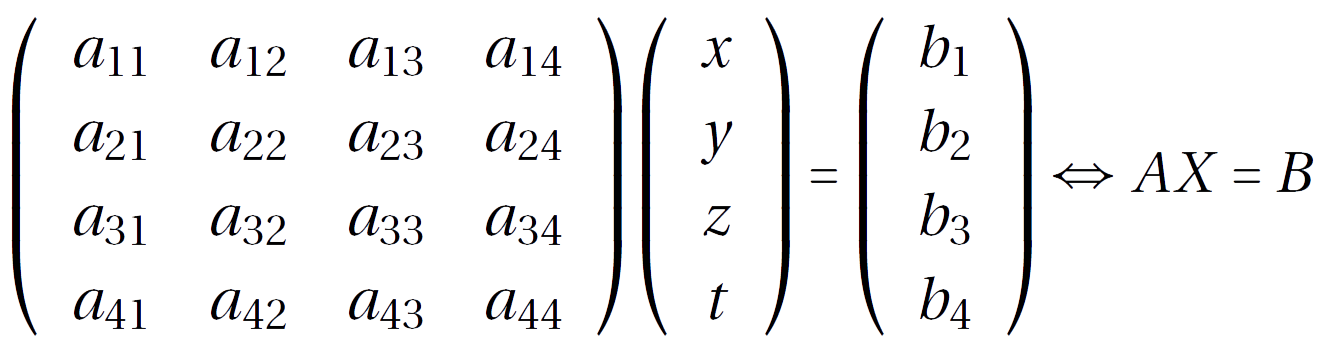
Khi đó nghiệm của hệ viết dưới dạng ma trận là:

$latex X = A^{-1}B$

About Bitex_PTGD

Đam mê toán học. Quản trị viên Diễn Đàn Toán Casio. Mọi thắc mắc, quý thầy cô và các bạn học sinh vui lòng liên hệ vào hộp thư Inbox tại Fanpage: Diễn Đàn Toán Casio.