BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Ứng dụng Phương trình đẳng cấp bậc 2 tìm biểu thức đúng
- 13/12/2017
- 399 lượt xem
Giải sử ta có hệ thức [latex]{a^2} + {b^2} = 7ab[/latex] với [latex]a,b>0[/latex] . Hệ thức nào sau đây đúng.
A) [latex]2{\log _2}\left( {\frac{{a + b}}{3}} \right) = {\log _2}a + {\log _2}b[/latex]
B) [latex]{\log _2}\left( {\frac{{a + b}}{3}} \right) = 2\left( {{{\log }_2}a + {{\log }_2}b} \right)[/latex]
C) [latex]2{\log _2}\left( {a + b} \right) = {\log _2}a + {\log _2}b[/latex]
D) [latex]4{\log _2}\left( {\frac{{a + b}}{6}} \right) = {\log _2}a + {\log _2}b[/latex]
Giải:
Đánh giá hệ thức [latex]{a^2} + {b^2} = 7ab[/latex] là một hệ đẳng cấp bậc 2.
Ta đặt [latex]a=kb[/latex] khi đó ta được [latex]{k^2}{b^2} + {b^2} – 7k{b^2} = 0 \Leftrightarrow {b^2}({k^2} – 7k + 1) = 0 \Leftrightarrow {k^2} – 7k + 1 = 0[/latex]
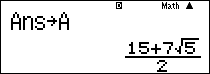
Chọn [latex]k = \frac{{7 + \sqrt 5 }}{2} \Rightarrow a = \frac{{7 + \sqrt 5 }}{2}b[/latex]
B1: Chọn [latex]b = \sqrt 5 \Rightarrow a = \frac{{7 + \sqrt 5 }}{3} \times \sqrt 5[/latex]
B2: Lưu a vào ô nhớ A, lưu b vào ô nhớ B
B3: Thử các đáp án
- Thử đáp án A ta được nhập biểu thức [latex]2{\log _2}\left( {\frac{{A + B}}{3}} \right) – {\log _2}A – {\log _2}B[/latex]
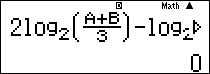
- Vậy chọn được đán A
About toancasiobitex
