BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
QUY TẮC 72 VÀ GIẢI QUYẾT BÀI TOÁN TÀI CHÍNH TRÊN CASIO FX 9860GII SD
- 07/07/2019
- 492 lượt xem
| Giả sử ta có một khoản đầu tư với giá trị hiện tại là $P$ và dự định mở một tài khoản ngân hàng với lãi suất hàng năm là $i$. Ta muốn tính thời gian để giá trị tương lai gấp đôi giá trị hiện tai, nghĩa là $F=2P$. Giả sử $5\% \leqslant i \leqslant 12\%$ là lãi suất phổ biến ở nước ta. |
Xem phương trình $$F=P(1+i)^n \Leftrightarrow \dfrac{F}{P}=(1+i)^n$$
Ở đây $n$ là số kỳ hạn (tính bằng năm) và $i$ là lãi kép hàng năm. Đặt $I=100i$ là số đứng trước dấu phần trăm.
Khi đó $F=2P \Leftrightarrow (1+i)^n=2 \Leftrightarrow n=\log_{1+i}2$
Ta muốn tính $n.I$. Muốn vậy ta xét hàm số $f(x)=100x.\log_{1+x}2$, ở đây ta ký hiệu $x=i$.
Mở MENU 8 nhập hàm $f(x)=100x.\log_{1+x}2$ sau đó SET để xác định BEGIN, END và STEP. Ưu thế của máy tính Casio fx-9860 GII SD là nó nhận 999 giá trị thuộc tập xác định, phép phân hoạch này đủ mịn để có kết quá chính xác gần như tuyệt đối.
Duyệt bảng ta thấy nếu lãi suất $i$ từ $6,37\%$
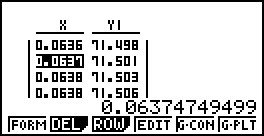
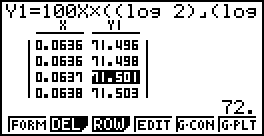
đến $9,33\%$
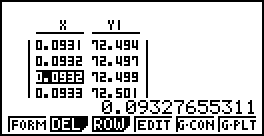
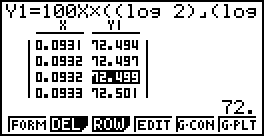
thì tích của số kỳ hạn (theo năm) với lãi suất $I$ (đứng trước dấu %) luôn luôn bằng 72 (làm tròn đến đơn vị).
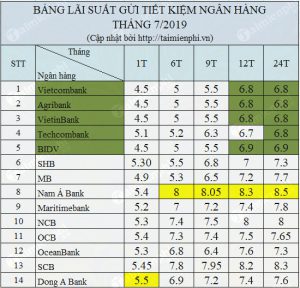
Với lãi suất phổ biến ở nước ta từ 6% (của ngân hàng nhà nước) đến 9% (của các ngân hàng thương mại) thì quy luật này luôn đúng.
|
Vậy thời gian để một giá trị hiện tại khi đầu tư vào một quỹ tín dụng (hay một tài khoản ngân hàng ngân hàng) tăng lên gấp đôi bằng tỉ số của số 72 và số đứng trước dấu phần trăm của lãi kép hàng năm. |
Một cách phát biểu khác
|
Để một giá trị hiện tại khi đầu tư vào một quỹ tín dụng (hay một tài khoản ngân hàng ngân hàng) tăng lên gấp đôi thì số đứng trước dấu % của lãi kép hàng năm phải bằng tỉ số của số 72 và số kỳ hạn hàng năm. |
Ví dụ 1:
| Nếu đầu tư 100.000.000 VNĐ vào một tài khoản ngân hàng với lãi suất 8% hàng năm thì sau bao lâu số dư của tài khoản nói trên sẽ tăng gấp đôi (thành 200.000.000 VNĐ). |
Trả lời: Vào khoảng $\dfrac{72}{8}=9$ (năm)
Ví dụ 2:
| Nếu cần đầu tư một khoản tiền vào ngân hàng để sau 11 năm số dư tài khoản sẽ tăng lên gấp đôi thì lãi suất phải là bao nhiêu?. |
Trả lời: $\dfrac{72}{11}\approx 6,55\%$
Có thể tham khảo thêm trong bảng tính dưới đây: $n.I$ đã làm tròn đến đơn vị.
Loading…
Reload document 
Open in new tab About TS. Nguyễn Thái Sơn
