Tam giác đều ABC và hình vuông ADEF cùng nội tiếp đường tròn (O;R)

Đề bài: Cho tam giác đều ABC và hình vuông ADEG cùng nội tiếp đường tròn (O; R). Tính diện tích phân chung của tam giác và hình vuông.

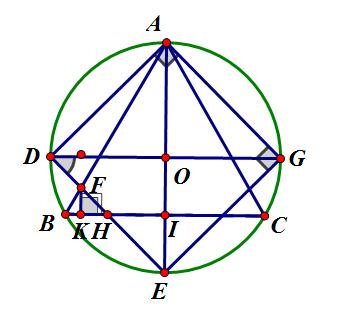
Ta có [latex]OI=IE=HI=\dfrac{R}{2}[/latex].
[latex]BI = \dfrac{{AI}}{{\tan \widehat {ABI}}} = \dfrac{{AI}}{{\tan 60}} = \dfrac{{R + \dfrac{R}{2}}}{{\sqrt 3 }} = \dfrac{{R\sqrt 3 }}{2}[/latex] Suy ra [latex]BH = BI – HI = \dfrac{{R\sqrt 3 }}{2} – \dfrac{R}{2} = \dfrac{R}{2}\left( {\sqrt 3 – 1} \right)[/latex] Gọi các giao điểm như trên hình vẽ. Kẻ FK vuông góc với BH, đi tính diện tích tam giác FBH.
Ta có:
[latex]\begin{array}{l}
\left\{ \begin{array}{l}
BK = FK.\cot \widehat {FBK}\\
HK = FK.\cot \widehat {FHK}
\end{array} \right. \Rightarrow BH + HK = FK.\left( {\cot \widehat {FBK} + \cot \widehat {FHK}} \right)\\
\Rightarrow FK = \dfrac{{BH}}{{\cot \widehat {FBK} + \cot \widehat {FHK}}} = \dfrac{{\dfrac{R}{2}\left( {\sqrt 3 – 1} \right)}}{{\cot 60 + \cot 45}} = \dfrac{{R\sqrt 3 }}{2}\left( {\dfrac{{\sqrt 3 – 1}}{{\sqrt 3 + 1}}} \right)\\
\Rightarrow {S_{FBH}} = \dfrac{1}{2}FK.BH = \dfrac{{R\sqrt 3 }}{4}\left( {\dfrac{{\sqrt 3 – 1}}{{\sqrt 3 + 1}}} \right).\dfrac{R}{2}\left( {\sqrt 3 – 1} \right) = \dfrac{{{R^2}\sqrt 3 }}{8}\dfrac{{{{\left( {\sqrt 3 – 1} \right)}^2}}}{{\sqrt 3 + 1}}
\end{array}[/latex]

Vậy diện tích miền chung cần tìm là:
[latex]S = {S_{ABC}} – 2{S_{FBH}} = \dfrac{1}{2}.\dfrac{{3R}}{2}.R\sqrt 3 – 2\dfrac{{{R^2}\sqrt 3 }}{8}\dfrac{{{{\left( {\sqrt 3 – 1} \right)}^2}}}{{\sqrt 3 + 1}} = {R^2}\left( {\dfrac{{3\sqrt 3 }}{4} – \dfrac{{\sqrt 3 }}{4}.\dfrac{{{{\left( {\sqrt 3 – 1} \right)}^2}}}{{\sqrt 3 + 1}}} \right)[/latex]

About TailieuCasio