TÌM SỐ TỰ NHIÊN MÀ LẬP PHƯƠNG CÓ TẬN CÙNG LÀ 4 SỐ CHO TRƯỚC

Lấy ví dụ câu 5 đề thi chọn đội tuyển TP HCM năm học 2015-2016

Tìm số tự nhiên nhỏ nhất sao cho lập phương của nó có tận cùng là 4 chữ số 1.

Gợi ý:

1. Ta có nhận xét có duy nhất một chữ số mà lập phương bằng 1 đó là số 1.
2. Xét số có hai chữ số với chữ số đơn vị là 1 và lập phương số đó 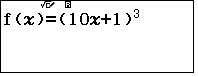ta có duy nhất một số mà lập phương của nó có tận cùng là 11 đó là số 71: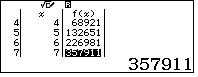   
3. Xét số có ba chữ số với chữ số chục là 7 và đơn vị là 1 và lập phương số đó
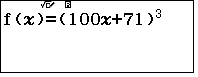   ta có duy nhất một số mà lập phương có tận cùng 111, đó là số 471: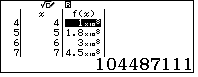
4. Xét số có bốn chữ số với chữ số trăm là 4, chữ số chục là 7 và đơn vị là 1 và lập phương số đó, nhận xét rằng $(471+1000x)^3=471^3+3\times 471^2\times 1000x+ 3\times (1000x)^2\times 471+(1000x)^3$ nên ta chỉ xét bộ phận $471^3+3\times 471^2\times 1000x$ kết quả 
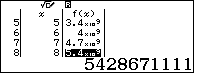
5. Vậy số cần tìm là 8471.

Lưu ý dành cho GV phụ trách đội tuyển:

• Trong các bảng trên ta đều chọn phạm vi là
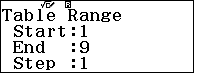
• Các hằng đẳng thức

$(1+10x)^3=1^3+3\times 10x +3(10x)^2+(10x)^3$

$(71+100x)^3=71^3+3\times 71^2\times 100x+3\times (100x)^2\times 71+(100x)^3$

$(471+1000x)^3=471^3+3\times 471^2\times 1000x+ 3\times (1000x)^2\times 471+(1000x)^3$

cho ta nhận xét rằng các số $1^3, 71^3, 471^3$ bảo lưu được các chữ số 1 tận cùng cho phép lập phương tiếp theo. 

• Ta tiếp tục theo tiến trình này 

$(8471+10000x)^3=8471^3+3\times 8471^2\times 10000x+ \dots$

vì $8471^3=5428671111$ nên ta muốn tìm $x \in \{1,2,3,4,5,6,7,8,9\}$ sao cho chữ số đơn vị của phép tính $3\times 8471^2x$ là chữ số 4.  

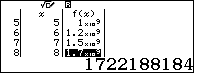
Vậy số tự nhiên nhỏ nhất mà lập phương của nó có tận cùng là 5 chữ số 1 là số 88471 và $88471^3=6924729425$11111

• Ta muốn tìm $x \in \{1,2,3,4,5,6,7,8,9\}$ sao cho chữ số đơn vị của phép tính $3\times 88471^2x$  là chữ số 6

  Với $x=1$ ta có

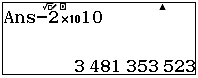
  Với 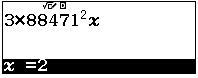ta có

  $x=2$ là số cần tìm.

Vậy số tự nhiên nhỏ nhất mà lập phương của nó có tận cùng là 6 chữ số 1 là số 288471.

$$288471^3=24005263647111111$$

HẾT

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.