BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Một cách chứng minh tứ giác nội tiếp
- 21/07/2021
- 249 lượt xem
Thông thường ta chứng minh tứ giác $ABCD$ nội tiếp như sau (tuỳ theo trường hợp).
- 1. $A$ và $D$ cùng nhìn $BC$ dưới 1 góc vuông. Khi đó tứ giác $ABCD$ nội tiếp đường tròn đường kính $BC$. Tổng quát, nếu $A$ và $D$ cùng nhìn $BC$ dưới cùng một góc thì tứ giác $ABCD$ nội tiếp.
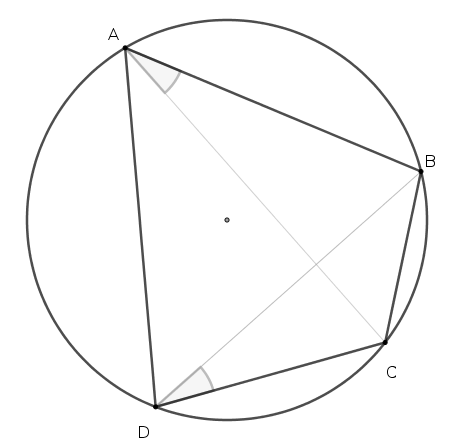
- 2. Hai góc đối diện của tứ giác bù nhau.
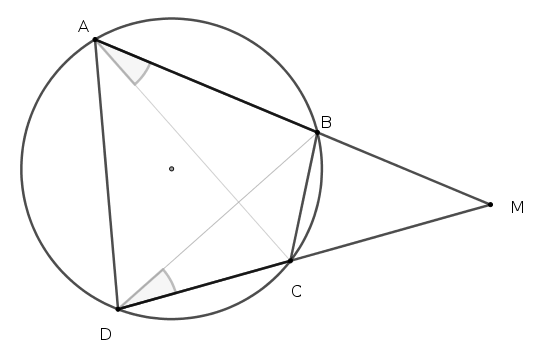
- 3. Một góc trong của tứ giác đó bằng góc ngoài của góc đối diện.
Cả ba trường hợp nói trên đều sử dụng góc. Trong khuôn khổ lớp 9, ít khi nào học sinh sử dụng đến hệ thức lượng. Nếu có sử dụng thì cũng đưa về tam giác đồng dạng để dẫn đến hai góc bằng nhau.
Trong bài thi vào lớp 10 năm 2021 của TP Đà Nẵng có nhiều bài toán tính toán phức tạp. Để có thể chứng minh tứ giác nội tiếp, chúng tôi cho rằng nên đưa thêm tiêu chuẩn tứ giác nội tiếp dựa vào hệ thức lượng như sau:
Áp dụng
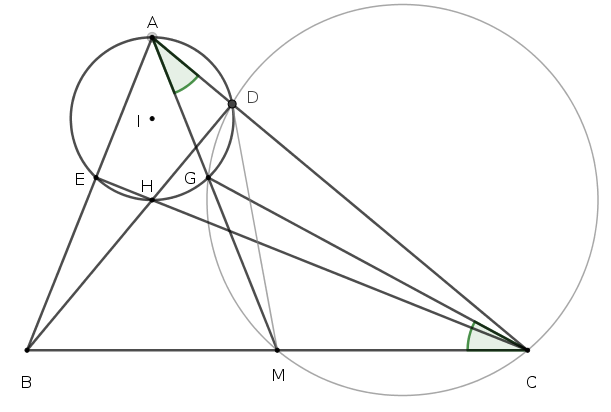
Bước 1: Chứng minh $\mathbf{MD}$ là tiếp tuyến của đường tròn đường kính $\mathbf{AH}$.
Suy ra $\widehat{MAC}=\widehat{MDG}$ (cùng chắn cung $DG$) (1)
Bước 2: Chứng minh tứ giác $\mathbf{CDGM}$ nội tiếp.
Suy ra $\widehat{MDG}=\widehat{GCM}$ (cùng chắn cung $GM$) (2)
Từ (1) và (2) ta suy ra $\widehat{MAC}=\widehat{GCM}$.
\begin{align*}\widehat{MDI}&=\widehat{MDB}+\widehat{BDI}\ \text{trong đó}\ \left\lbrace\begin{array}{l} \widehat{MDB} = \widehat{MBD}\\ \widehat{BDI} = \underbrace{\widehat{IHD}=\widehat{BCD}}_{\text{góc có các cạnh vuông góc}}\end{array}\right.\\
&=\widehat{MBD}+\widehat{BCD}=90^\circ\end{align*}
- $\bullet\ $ Tứ giác $EBCD$ nội tiếp nên $\widehat{EBC}=\underbrace{\widehat{ADE}=\widehat{AGE}}_{\text{cùng chắnn cung AE}}$
- $\bullet\ $ Do đó tứ giác $EBGM$ nội tiếp, suy ra $AE.AB=AG.AM$. Ngoài ra Tứ giác $EBCD$ nội tiếp nên nên $$AE.AB=AD.AC$$
- $\bullet\ $ Do đó $AG.AM=AD.AC$ suy ra tứ giác $MGDC$ nội tiếp (đpcm)
PS. Thầy Sơn không giỏi giải Toán lớp 9 bằng các Thầy/cô dạy lớp 9 nên mới phải đưa nhiều tiêu chuẩn cho tứ giác nội tiếp để sử dụng. Đối với học sinh cũng vậy, nếu các em dự tuyển vào trường top trên, các thầy cô cũng nên hướng dẫn thêm cho các em về tiêu chuẩn này, phòng khi gặp bài toán khó (như bài toán Hình học của Đà Nãng là khó). GV Đà Nẵng họ nói “vừa sức” nhưng các em khẳng định khó từ câu 2B. Tất nhiên có vài em được điểm 10 rất đáng khen.
About TS. Nguyễn Thái Sơn
