MỘT SỐ BÀI TOÁN VỀ NHỊ THỨC NEWTON TRONG ĐỀ THI HSG MÁY TÍNH CẦM TAY- PHẦN 1
- 12/07/2022
- 1,244 lượt xem
Bài 1. Tìm hệ số lớn nhất trong khai triển nhị thức ${{(5x+\sqrt{7})}^{11}}$
Hướng dẫn giải
Ta có \[{{(5x+\sqrt{7})}^{11}}=\sum\limits_{k=0}^{11}{C_{11}^{k}{{(5x)}^{k}}{{(\sqrt{7})}^{11-k}}}=\sum\limits_{k=0}^{11}{C_{11}^{k}{{5}^{k}}{{(\sqrt{7})}^{11-k}}}{{x}^{k}}\]
Hệ số của số hạng tổng quát ${{a}_{k}}=C_{11}^{k}{{.5}^{k}}{{(\sqrt{7})}^{11-k}};k\in \mathbb{Z},0\le k\le 11$
Xét
$\dfrac{{{a}_{k}}}{{{a}_{k+1}}}<1$$\Leftrightarrow \dfrac{C_{11}^{k}{{.5}^{k}}.{{(\sqrt{7})}^{11-k}}}{C_{11}^{k+1}{{.5}^{k+1}}.{{(\sqrt{7})}^{10-k}}}<1$ $\Leftrightarrow \dfrac{\sqrt{7}}{5}.\dfrac{k+1}{11-k}<1$ $\Rightarrow k<6,8$
$\dfrac{{{a}_{k}}}{{{a}_{k+1}}}>1$$\Leftrightarrow \dfrac{C_{11}^{k}{{.5}^{k}}.{{(\sqrt{7})}^{11-k}}}{C_{11}^{k+1}{{.5}^{k+1}}.{{(\sqrt{7})}^{10-k}}}>1$$\Leftrightarrow \dfrac{\sqrt{7}}{5}.\dfrac{k+1}{11-k}>1$$\Rightarrow k>6,8$
Vì $k\in \mathbb{Z},0\le k\le 11$ nên ta có: ${{a}_{0}}<{{a}_{1}}<…<{{a}_{6}}$ và ${{a}_{7}}>{{a}_{8}}>…>{{a}_{11}}$
Mặt khác $\dfrac{{{a}_{6}}}{{{a}_{7}}}=\dfrac{\sqrt{7}}{5}.\dfrac{7}{5}<1\Rightarrow {{a}_{6}}<{{a}_{7}}$
Từ đó suy ra $\max \{{{a}_{k}}\text{ }\!\!\}\!\!\text{ }={{a}_{7}}=C_{11}^{7}{{.5}^{7}}.{{(\sqrt{7})}^{4}}$
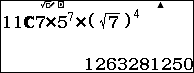
Bài 2. Cho khai triển nhị thức (a + b)n với a, b ¹ 0 theo công thức Niu-tơn. Gọi ba số hạng thứ nhất, thứ hai, thứ ba của khai triển lần lượt là $p,\,\,q,\,\,r.$ Biết $17{{q}^{2}}=36pr.$Tính tổng S tất cả các hệ số của khai triển.
Hướng dẫn giải
\[{{\left( a+b \right)}^{n}}=\sum\limits_{k=0}^{n}{C_{n}^{k}{{a}^{n-k}}{{b}^{k}}}\]
Ba số hạng đầu tiên theo thứ tự là $p=C_{n}^{0}{{a}^{n}},q=C_{n}^{1}{{a}^{n-1}}b,r=C_{n}^{2}{{a}^{n-2}}{{b}^{2}}$
Từ giả thiết suy ra $17{{\left( C_{n}^{1}{{a}^{n-1}}b \right)}^{2}}=36.C_{n}^{0}{{a}^{n}}.C_{n}^{2}{{a}^{n-2}}{{b}^{2}}$
Hay $17{{\left( C_{n}^{1} \right)}^{2}}=36.C_{n}^{0}.C_{n}^{2}\Leftrightarrow 17{{n}^{2}}=36.\dfrac{n(n-1)}{2}$$\Leftrightarrow {{n}^{2}}-18n=0\Leftrightarrow n=18$
Tổng tất cả các hệ số của khai triển là $S$
\[S=C_{18}^{0}+C_{18}^{1}+…+C_{18}^{18}={{2}^{18}}= 262144\]
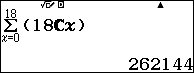 hoặc
hoặc 
Bài 3. Tính tổng \[S=2C_{18}^{1}+{{2}^{3}}C_{18}^{3}+{{2}^{5}}C_{18}^{5}+…+{{2}^{17}}C_{18}^{17}\].
Hướng dẫn giải
Cách 1.
Xét nhị thức ${{(1+x)}^{18}}=C_{18}^{0}+C_{18}^{1}x+C_{18}^{2}{{x}^{2}}+…+C_{18}^{17}{{x}^{17}}+C_{18}^{18}{{x}^{18}}$
x = 2 ta được ${{3}^{18}}=C_{18}^{0}+C_{18}^{1}3+…+C_{18}^{17}{{3}^{17}}+C_{18}^{18}{{3}^{18}}$ (1)
x = -2 ta được ${{(-1)}^{18}}=C_{18}^{0}-C_{18}^{1}3+…-C_{18}^{17}{{3}^{17}}+C_{18}^{18}{{3}^{18}}$ (2)…
Từ đó nên (1) – (2) ta được kết quả S
\[\,\,S=\dfrac{1}{2}({{3}^{18}}-1)=193710244\]

Cách 2.
\[S=2C_{18}^{1}+{{2}^{3}}C_{18}^{3}+{{2}^{5}}C_{18}^{5}+…+{{2}^{17}}C_{18}^{17}=\sum\limits_{x=0}^{8}{{{2}^{2x+1}}C_{18}^{2x+1}}\]
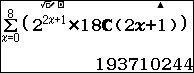
Mọi ý kiến đóng góp và các câu hỏi thắc mắc về các bài viết hướng dẫn giải toán casio cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay