LẬP BẢNG TÌM GTLN VÀ GTNN TRÊN CASIO FX 580VNX

Ví dụ sau đây chọn Câu 10 trong Đề thi chọn đội tuyển TPHCM năm học 2015-2016:

Tìm gần đúng (chính xác đến 4 chữ số thập phân) GTNN của hàm số
$$y=\dfrac{1.2x+5.9}{\sqrt{2.3x-7.4}}$$

• Cài đặt bảng với chế độ một hàm số để tận dụng 45 giá trị.
• Bấm Menu 8 và nhập hàm số
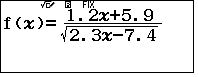
• Phạm vi 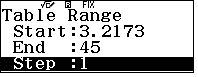($\dfrac{7.4}{2.3} \approx 3.2173$)
• Duyệt bảng tìm GTNN trong bảng, giá trị này trong khoảng
  
  ứng với $x=11.2173913, x=12.2173913$
• Tinh chỉnh với phạm vi hẹp hơn 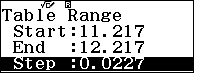ta có GTNN nằm trong khoảng mới
• Định dạng số với 4 chữ số thập phân và tinh chỉnh lần hai,
   
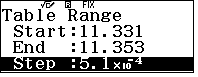
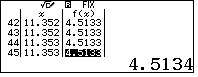
  45 giá trị của $x$ đều cho $f(x)$ là  4.5134.
• Ta kết luận GTNN của hàm số là $\min y =4.5134$.

PS.

1. Cách giải trên chỉ thực hiện trong kỳ thi HSG MTCT với yêu cầu cơ bản là hàm số đã cho chỉ có một điểm cực trị. Đối với GV phụ trách đội tuyển, các thầy/cô lưu ý khi bình phương hai vế, ta có hàm số hữu tỉ bậc 2 /bậc 1 có đồ thị là một hyperbol xiên góc. Với nhánh phải (do $x \geqslant \dfrac{7}{4}$) hàm số chỉ có cực tiểu và GTNN là giá trị cực tiểu.
2. Yêu cầu cao hơn bắt buộc phải tính toán chi tiết như sau:

   $$y=\dfrac{1.2x+5.9}{\sqrt{2.3x-7.4}} \Rightarrow 1.2^2x^2+(2\times 1.2 \times 5.9 -2.3 y^2)x+5.9^2+7.4y^2=0$$

   $\Delta=(2\times 1.2 \times 5.9 -2.3 y^2)^2-4\times 1.2^2\times (5.9^2+7.4y^2)$

   Bấm máy tính Casio fx-580VN X giải bất phương trình bậc 4 theo biến $y$.
   

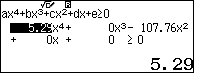
3. Kết quả 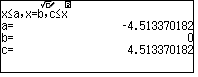do điều kiện $x > \dfrac{7.4}{2.3}$ nên $y > 0$, do đó $\min y=4.5134$

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.