BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Giải toán tìm số dư trong phép chia
- 23/10/2017
- 2,752 lượt xem
Tìm dư của phép chia [latex]{234567891^{12}}[/latex] cho [latex]123456789[/latex]
Áp dụng [latex]{{(a+b)}^{n}}\equiv {{b}^{n}}\text{ }\left( \bmod m \right)[/latex] với [latex]a\vdots m[/latex]
Giải bài toán trên:
Tính
[latex]234567891\equiv 111111102(\bmod 123456789)\text{ }[/latex]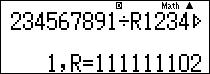
Vậy
[latex]{{234567891}^{12}}\equiv {{111111102}^{12}}(\bmod 123456789)\text{ }[/latex]Mà
[latex]\begin{array}{l} {111111102^2}\\ = {\left( {111111100 + 2} \right)^2}\\ = {111111100^2} + 444444400 + 4\\ = 12345676543210000 + 444444404\\ \Rightarrow {111111102^2} = 12345676987654404 \end{array}[/latex]Ta thực hiện chia:
Tìm số dư của [latex]12345676987654404[/latex] khi chia cho 123456789.
Cách 1: Dùng phím :R. Vì phím R chỉ thực hiện tìm dư khi chia một số có tối đa là 10 chữ số cho một số có tối đa là 10 chữ số nên việc sử dụng phím R trong trường hợp này mất nhiều thời gian cho việc nối-ghép số khi chia vì phải nhập đi nhập lại vào số lượng chữ số khá nhiều.
Cách 2: Có thể chia trực tiếp tận dụng máy có bộ nhớ lưu trữ tối đa là 15 chữ số.
Cách 3: Có thể dùng phím Ing với vòng lặp sau: (người đọc tự phát hiện quy luật):
[latex]A=A{{.10}^{2}}+B-Int\left( \left( A{{.10}^{2}}+B \right)\div 123456789 \right)\times 123456789[/latex]Với A nhập vào là [latex]123456769, B=87[/latex].
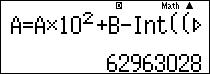
Vậy bài toán chuyển về tìm dư của [latex]{{62963028}^{6}}[/latex] khi chia [latex]123456789[/latex].
Thực hiện tương tự và thu được kết quả số dư cần tìm là [latex]54306099[/latex].
About TailieuCasio
