BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
GIẢI QUYẾT MỘT SỐ BÀI TOÁN THỰC TẾ VỀ KHOẢNG CÁCH TRONG CT THCS 2019-2020
- 15/10/2019
- 1,310 lượt xem
Câu 1. Tính chiều cao của đài kiểm soát không lưu Nội Bài. Biết bóng của đài kiểm soát được chiếu bởi ánh sáng mặt trời xuống đất dài $200$ m và góc tạo bởi tia sáng với mặt đất là $25^\circ24’$ (kết quả làm tròn đến hàng đơn vị).
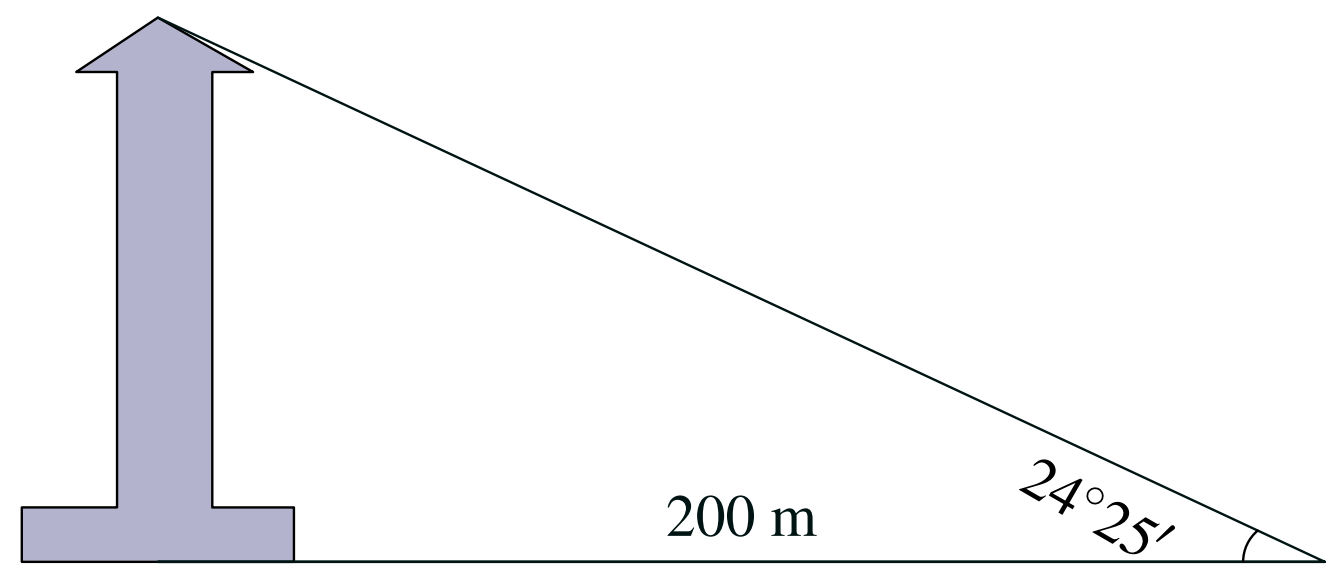
| A. $86$ m. | B. $221$ m. | C. $181$ m. | D. $95$ m. |
Hướng dẫn
Không mất tính tổng quát, giả sử đài kiểm soát không lưu là đoạn thẳng $AB$, bóng của nó trên mặt đất là đoạn thẳng $AC$ (như hình vẽ).
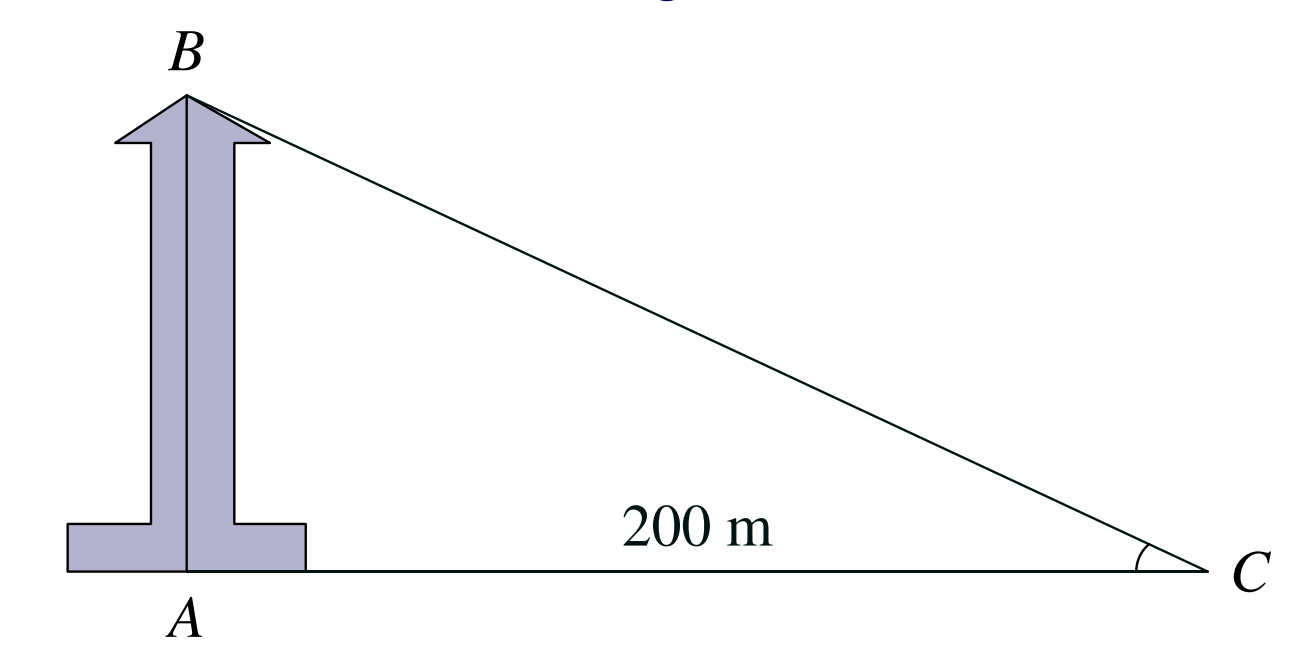
Tam giác $ABC$ vuông tại $A$, có $AC=200$ m, $\widehat{BCA}=25^\circ24’$. Chiều cao của đài kiểm soát là
\[AB=AC\cdot \tan \widehat{BCA}=200\cdot \tan 25^\circ24’\approx 95 \text{ (m)}.\]
Chọn câu D.
Câu 2. Quãng đường $AB$ dài $60$ km, một người đi xe đạp từ $A$ đến $B$ với vận tốc và thời gian quy định. Sau khi đi được nửa quãng đường người đó giảm vận tốc $5$ km/h trên nửa quãng đường còn lại. Vì vậy, người đó đã đến $B$ chậm hơn quy định $1$ giờ. Tính vận tốc và thời gian quy định của người đó.
Hướng dẫn
Gọi vận tốc quy định của người đó là $x$ (km/h), ($x>5$).
Suy ra thời gian quy định để người đó đi hết quãng đường là $\dfrac{60}{x}$ (h).
Nửa quãng đường đầu là $\dfrac{60}{2} = 30$ (km) nên thời gian đi nửa quãng đường đầu là $\dfrac{30}{x}$ (h).
Nửa quãng đường sau, vận tốc người đó giảm $5$ km/h nên vận tốc trên nửa quãng đường sau là $x-5$ (km/h).
Suy ra thời gian đi nửa quãng đường sau là $\dfrac{30}{x-5}$ (h).
Vì người đó đến chậm so với thời gian quy định là $1$ giờ nên ta có phương trình.
Vậy vận tốc quy định của người đó là $15$ km/h và thời gian quy định của người đó là $60:15=4$ giờ.
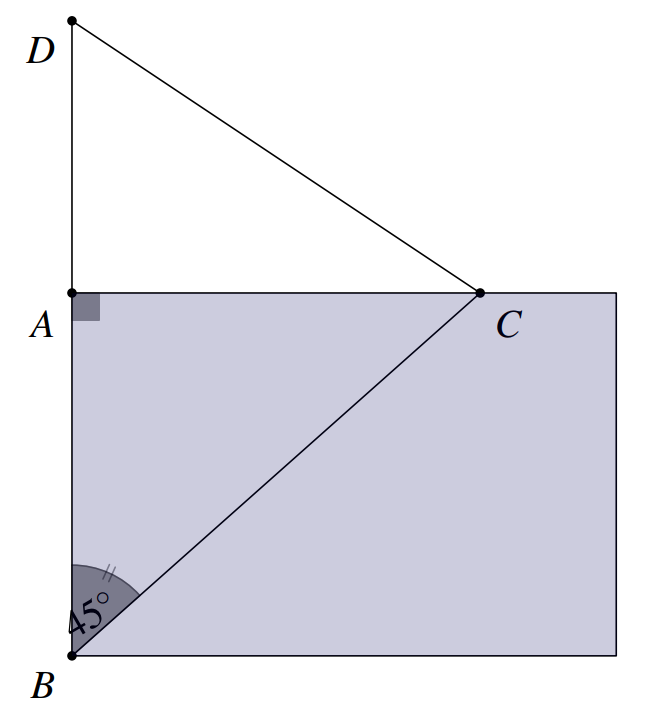
Câu 3. Từ nhà bạn An đến trường học, bạn phải đi đò qua một khúc sông rộng $173{,}2$ m đến điểm $A$ (bờ bên kia), rồi từ $A$ đi bộ đến trường tại điểm $D$ (ở hình bên). Thực tế, do nước chảy nên chiếc đò bị dòng nước đẩy xiên một góc $ 45^\circ $ đưa bạn tới điểm $C$ (bờ bên kia). Từ $C$ bạn An đi bộ đến trường theo đường $CD$ mất thời gian gấp đôi khi đi từ $A$ đến trường theo đường $AD$. Độ dài quãng đường $CD$ là (Giả sử vận tốc đi bộ của bạn An không thay đổi (chuyển động thẳng đều), kết quả làm tròn đến hàng đơn vị).
Hướng dẫn
Gọi thời gian bạn An đi bộ từ A đến trường theo AD là $ x $, vận tốc đi bộ là $ v $.
Khi đó, ta có $ CD=v\cdot 2x $ và $ AD=v\cdot x $. Từ đó, suy ra $ CD=2AD $.
Xét tam giác $ ABC $ vuông tại $ A $ và có $$ \widehat{ABC}=45^\circ $, $ AC=173,2 \text{m}$$
Suy ra $$ AC=AB=173,2 \text{m}$$
Xét tam giác $ ADC $ vuông tại $ A $, có
\begin{align*}
CD^2=AD^2+AC^2 &\Rightarrow AC=AD\cdot \sqrt{3}\\
&\Rightarrow AD=\dfrac{AC}{\sqrt{3}}\\
&\Rightarrow CD=2\cdot \dfrac{173{,}2}{\sqrt{3}}\approx 200 \text{(m)}
\end{align*}
Nguồn: Sưu tầm
About Bitex Khánh Vũ
