BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Mời giải toán tứ giác nội tiếp
- 02/12/2020
- 180 lượt xem
Thầy Sơn mời các bạn tham gia giải bài toán sau đây:
| Cho tam giác $ABC$ nội tiếp đường tròn tâm $O$ và ngoại tiếp đường tròn $(C)$ tâm $I$. Gọi $d$ là đường thẳng song song với $BC$ và tiếp xúc với đường tròn $(C)$. $X$ là điểm trên $d$ sao cho $X, I, O$ thẳng hàng.Đường thẳng vuống góc với $IX$ tại $I$ cắt $d$ tại $Y$. Chứng minh tứ giác $AXOY$ nội tiếp. |
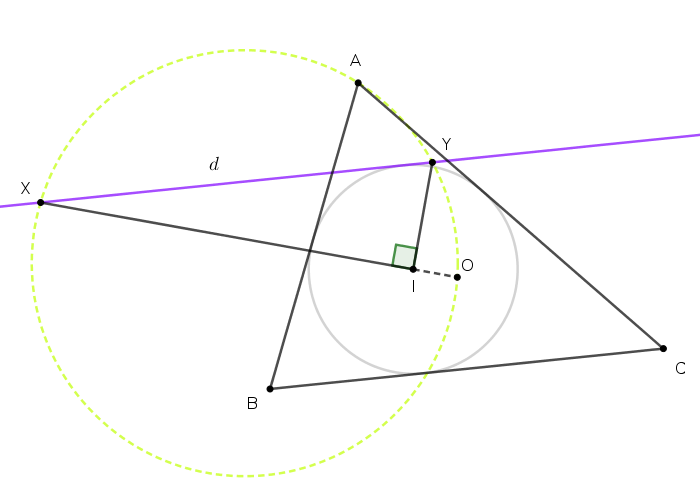
Các bạn có thể sử dụng số phức. Riêng thầy Sơn sẽ dùng máy tính Casio FX-580 VNX để tính toán và kết luận. Các bạn mô phỏng tính toán của thầy để viết lời giải tự luận.
Hướng dẫn: Trong mặt phẳng tọa độ cho 4 điểm phân biệt $A, B, C, D$. Khi đó tứ giác $ABCD$ nội tiếp khi và chỉ khi $$\dfrac{c-a}{c-b}:\dfrac{d-a}{d-b}$$
là số thực. Ở đây $a, b,c, d$ lần lượt là các số phức biểu diễn các điểm $A, B, C, D$ tương ứng và dấu : là ký hiệu phép chia.
Chia sẻ
About TS. Nguyễn Thái Sơn
