Bài toán về phép giải tam giác trong bài thi HSG MTCT cấp THCS (tiếp theo)
- 07/09/2020
- 542 lượt xem
Bài 9. Cho tam giác ABC có các góc $latex A , C$ nhọn; $latex BC =3, 5$; đường cao $latex BH =2, 7$ và bán kính đường tròn ngoại tiếp bằng 2, 8 . Gọi $latex K$ là giao điểm của $latex BH$ và trung tuyến $latex AM$. Tính (chính xác đến 2 chữ số thập phân):
|
Giải
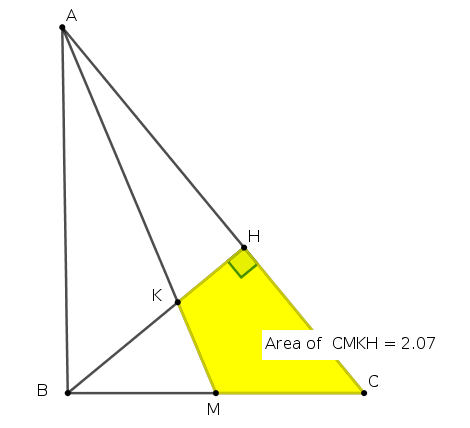
1) Ta có công thức tính bán kính đường tròn ngoại tiếp tam giác
$R=\dfrac{abc}{4S}=\dfrac{BC.CA.AB}{2.BH.AC}\Rightarrow AB=\dfrac{2BH.R}{BC}$=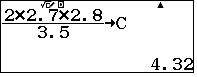
Vì các góc $A$ và $C$ đều nhọn nên $H$ nằm trên đoạn $AC$.
Vậy $AC=AH+HC=\sqrt{AB^2-BH^2}+\sqrt{BC^2-BH^2}$=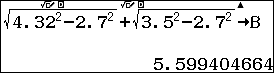

Trung tuyến $AM=\sqrt{\dfrac{B^2+AC^2-\dfrac{BC^2}{2}}{2}}$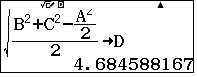
2) Bán kính đường tròn ngoại tiếp tam giác $ABM$
$$R_{ABM}=\dfrac{AM}{2\sin B}=\dfrac{AM}{2\sin\left(\arccos\dfrac{BA^2+BC^2-AC^2}{2BA.BC}\right)}$$
3) Tính diện tích tứ giác $CMKH$
Ta có $b=\dfrac{CM}{CB}=\dfrac12$ lưu vào B.
$a=\dfrac{AH}{AC}=$
Áp dụng công thức đã xây dựng trong bài trước ta có
$\dfrac{AK}{AM}=\dfrac{1-a}{1-ab}$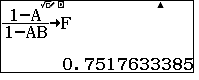
Ta có:
$BH.AC=BC.d(A,BC)\Rightarrow d(A,BC)=$
$S_{CMKH}=S_{AMC}\left(1-\dfrac{AK}{AM}\times \dfrac{AH}{AC}\right)$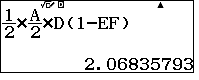
 BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay