VỀ MỘT BÀI TOÁN GIẢI PHƯƠNG TRÌNH BẬC HAI

Câu hỏi của một bạn gửi thầy Sơn về vấn đề chuyển kết quả từ số thập phân sang biểu thức chứa căn trên máy tính Casio fx 580VNX. Mời các bạn theo dõi và cho ý kiến đóng góp.

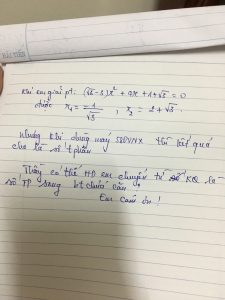
Phương trình: $$(\sqrt3-3)x^2+4x+1+\sqrt3=0$$

Đây là trường hợp các hệ số phức tạp nên gần như không có 1 hướng đi nào chung cho trường hợp này.

Với bài toán như thế này, theo chúng tôi có 2 hướng giải quyết cho nó:

1. Hướng 1: Lưu lại các nghiệm vào các ẩn $x_1=A;x_2=B$, rồi ra phương thức tính toán thông thường để biến đổi sơ cấp các ẩn A,B và tìm ra số chính xác(Một số hướng biến đổi sơ cấp nên sử dụng: $\sqrt{A^2}; \sqrt{B^2}; A+B;A.B$,….).

Với trường hợp của bài toán này

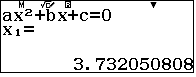
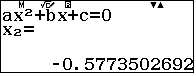
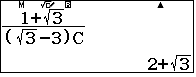
Vậy $x_1=2+\sqrt3, x_2=-\dfrac{\sqrt3}{3}$

–          Hướng 2: Dùng liên phân số. Lấy ví dụ là bài toán này.

Ta thấy $A$ là nghiệm của phương trình

$\dfrac{1}{\dfrac{1}{x-3}-1}=x-1 \Leftrightarrow x^2-4x+1=0 \Rightarrow x=2+\sqrt3$  lưu vào $D$.

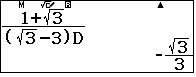
Nhận xét: Liên phân số giải quyết được hầu hết các số thập phân do một số vô tỉ sinh ra.

About TS. Nguyễn Thái Sơn

Nguyên trưởng Khoa Toán-Tin học ĐHSP TP HCM (1999-2009). /n Nguyên Giám đốc- Tổng biên tập NXB ĐHSP TP HCM (2009-2011). /n Nguyên Tổng thư ký Hội Toán học TP HCM (2008-2013). /n Giảng viên thỉnh giảng ĐHSP TP HCM.