BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
ỨNG DỤNG PHƯƠNG THỨC VECTOR ĐỂ TÍNH CÁC BÀI TOÁN TỔNG HỢP TRÊN CASIO FX580 VNX (VI)
- 16/12/2018
- 536 lượt xem
Ở loạt bài viết này chúng tôi đưa ra những hướng dẫn cụ thể từ dễ tới khó về phương thức vector trong máy tính Casio fx580VNX. Từ đó giúp các học sinh giải quyết những bài toán về hình học Oxyz và những bài toán về phương pháp tọa độ trong không gian một cách dễ dàng và nhanh chóng hơn. 3 Phần trước chúng ta đã nói về những tính năng về phương thức vector và một số ví dụ minh họa cho những tính năng đó. Phần này chúng ta sẽ tận dụng tối đa những tính năng của phương thức trên để áp dụng vào giải quyết nhiều vấn đề phức tạp trong hình học không gian hoặc phương pháp tọa độ trong không gian.
Phần 6: Ứng dụng phương thức vector để tính toán các bài toán tổng hợp
Tóm tắt: Ở loạt bài viết này chúng tôi đưa ra những hướng dẫn cụ thể từ dễ tới khó về phương thức vector trong máy tính Casio fx580VNX. Từ đó giúp các học sinh giải quyết những bài toán về hình học Oxyz và những bài toán về phương pháp tọa độ trong không gian một cách dễ dàng và nhanh chóng hơn. 3 Phần trước chúng ta đã nói về những tính năng về phương thức vector và một số ví dụ minh họa cho những tính năng đó. Phần này chúng ta sẽ tận dụng tối đa những tính năng của phương thức trên để áp dụng vào giải quyết nhiều vấn đề phức tạp trong hình học không gian hoặc phương pháp tọa độ trong không gian.
Xem lại: PHẦN 5 – ỨNG DỤNG PHƯƠNG THỨC VECTOR TRONG CASIO FX580 VNX(V)
7. Các bài toán tổng hợp
Câu 13. Cho hình lăng trụ tam giác đều $latex ABC.A’B’C’$ có cạnh bên bằng cạnh đáy. Đường vuông góc chung $latex d$ của $latex A’C$ và $latex BC’$ cắt tại . Tính tỉ số $latex \dfrac{NB}{NC’}$.
A. $latex \dfrac{3}{2}$. B. $latex \dfrac{2}{3}$. C. $latex 1$. D. $latex \dfrac{\sqrt{5}}{2}$
Chọn hệ trục tọa độ $latex Oxyz$ sao cho $latex O\equiv I$ ($latex I$ là trung điểm $latex BC$), tia $latex Ox$ đi qua $latex B$, tia $latex Oy$ đi qua $latex A$, tia $latex Oz$ hướng lên trên.
Giải
Khi đó $latex A’\left( 0;\dfrac{\sqrt{3}}{2};1 \right),C\left( -\dfrac{1}{2};0;0 \right),C\left( -\dfrac{1}{2};0;1 \right),B\left( \dfrac{1}{2};0;0 \right)$.
Ta có: $latex \left\{ \begin{align}& \overrightarrow{BC}=\left( -1;0;1 \right) \\& \overrightarrow{A’C}=\left( -\dfrac{1}{2};-\dfrac{\sqrt{3}}{2};-1 \right)//\overrightarrow{u}=\left( 1;\sqrt{3};2 \right) \\\end{align} \right.$
Nhập vector vào
Nhân 3 vector
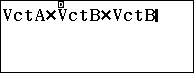
Phương trình mặt phẳng $latex \left( d,A’C \right)$ là: $latex 9x+\sqrt{3}y-6z=-\dfrac{9}{2}$
Tọa độ điểm $latex N$ là nghiệm của hệ phương trình:$latex \left\{ \begin{align}& x=\dfrac{1}{2}-t \\ & y=0 \\ & z=t \\ & 9x+\sqrt{3}y-6z=-\dfrac{9}{2} \\\end{align} \right.$
Nhập hệ phương trình vào và giải thôi
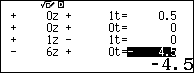
Suy ra $latex N\left( -\dfrac{1}{10};0;\dfrac{3}{5} \right)$. Vậy tỉ số $latex \dfrac{NB}{NC}=\dfrac{\sqrt{{{\left( \dfrac{1}{2}+\dfrac{1}{10} \right)}^{2}}+{{\left( \dfrac{3}{5} \right)}^{2}}}}{\sqrt{{{\left( -\dfrac{1}{2}+\dfrac{1}{10} \right)}^{2}}+{{\left( 1-\dfrac{3}{5} \right)}^{2}}}}$
Chọn phương thức tính toán thông thường w1 và bấm thôi
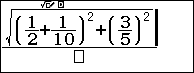
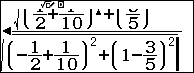
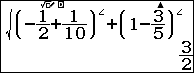
Vậy chọn đáp án A.
Câu 14. Trong không gian với hệ tọa độ $latex Oxyz$, cho hai đường thẳng
$latex {{d}_{1}}:\left\{ \begin{align} & x=1+t \\& y=2-2t \\& z=-3-t \\\end{align} \right.$ và $latex {{d}_{2}}:\left\{ \begin{align}& x=4+3t \\ & y=3+2t \\& z=1-t \\\end{align} \right.$
Trên đường thẳng $latex {{d}_{1}}$ lấy hai điểm $latex A,B$ thỏa $latex AB=3$. Trên đường thẳng $latex {{d}_{2}}$ lấy hai điểm $latex C,D$ thỏa $latex CD=4$. Tính thể tích $latex V$ của tứ diện $latex ABCD$.
A. $latex V=7$.
B. $latex V=2\sqrt{21}$.
C. $latex V=\dfrac{4\sqrt{21}}{3}$.
D. $latex V=\dfrac{5\sqrt{21}}{6}$.
Giải
Nhập ba vector sau đây vào máy tính:
$latex \overrightarrow{u}=\left( 1;-2;-1 \right),\overrightarrow{v}=\left( 3;2;-1 \right),\overrightarrow{MN}=\left( 3;1;4 \right)\left( M\left( 1;2;-3 \right)\in {{d}_{1}},N\left( 3;2;-1 \right)\in {{d}_{2}} \right)$
Ta có công thức
$latex {{V}_{ABCD}}=\dfrac{1}{6}AB.CD.d\left( AB,CD \right).\sin \left( AB,CD \right)$
Tính tích có hướng $latex \left[ \overrightarrow{u},\overrightarrow{v} \right]$
Khoảng cách giữa hai đường thẳng $latex AB,CD$ là $latex d\left( AB,CD \right)=\dfrac{\left| \left[ \overrightarrow{u},\overrightarrow{v} \right].\overrightarrow{MN} \right|}{\left| \left[ \overrightarrow{u},\overrightarrow{v} \right] \right|}$
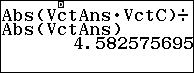
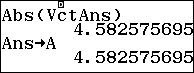
Sin của góc tạo bởi hai đường thẳng $latex AB,CD$ là
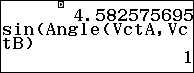
Sau đó chọn ra phương thức tính toán thông thường w1 để tính thể tích của khối tứ diện
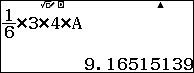
Vậy thể tích của khối tứ diện $latex ABCD$ là $latex 2\sqrt{21}\Rightarrow $ Chọn B.
—————————————————-
Trên đây là một số ví dụ tổng hợp về ứng dụng nhiều tính năng trên máy tính cầm tay (cụ thể là Casio fx-580VNX) để giải 1 số bài toán hình học tọa độ $Oxyz$ phức tạp. Tuy nhiên, máy tính không phải vạn năng, nên các bạn học sinh cũng nên chú ý vào học tập lí thuyết để có thể giải quyết được những bài toán khó nhằn. Chúc các bạn thành công.
Bài viết khó tránh khỏi thiếu sót, các bạn có thắc mắc hay bình luận hoặc góp ý thì đừng ngại gửi tin nhắn cho ad trên Fanpage: Diễn Đàn Toán Casio nhá.
Xem tiếp: TỔNG HỢP: ỨNG DỤNG PHƯƠNG THỨC VECTOR ĐỂ TÍNH TOÁN TRONG CASIO FX-580VNX
About Bitex Khánh Vũ
