BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
PHẦN 3: SỬ DỤNG CASIO FX 580VNX GIẢI QUYẾT CÁC BÀI TOÁN CĂN BẬC HAI CỦA SỐ PHỨC VÀ PHƯƠNG TRÌNH NGHIỆM PHỨC
- 06/01/2019
- 17,722 lượt xem
[dropshadowbox align=”none” effect=”lifted-both” width=”auto” height=”” background_color=”#ffffff” border_width=”1″ border_color=”#dddddd” ] PHẦN 3: CÁC BÀI TOÁN CĂN BẬC HAI CỦA SỐ PHỨC VÀ PHƯƠNG TRÌNH NGHIỆM PHỨC[/dropshadowbox]Số phức là một chuyên đề hay và tương đối khó, thường xuất hiện trong các đề thi THPT Quốc Gia những năm gần đây. Do đó, Diễn Đàn Máy Tính Cầm Tay chúng tôi sẽ gởi đến bạn đọc chuỗi các bài viết sử dụng máy tính Casio fx 580 vnx để giải quyết nhanh các bài toán về Số Phức. Chuyên đề này bao gồm các phần:
Phần 1: Sơ lược các tính năng Số phức trên máy tính Casio fx 580 vnx
Phần 2: Giải quyết các phép toán cơ bản về số phức
Phần 3: Căn bậc hai của số phức và phương trình nghiệm phức
Phần 4: Tìm đường thẳng biểu diễn tập hợp số phức
Phần 5: Tập hợp điểm biểu diễn số phức liên quan đến đường tròn
Phần 6: Tìm cực trị trên tập số phức
Phần 7: Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số bậc 3
Phần 8: Ứng dụng số phức vào phép tịnh tiến trong mặt phẳng
Phần 9: Ứng dụng số phức vào phép đối xứng trục và đối xứng tâm trong mặt phẳng
Bài toán 1: Tìm tham số $latex m$ để phương trình $latex 2{{z}^{2}}+\left( m-1 \right)z+\left( 2-m \right)=0$ có nghiệm $latex z=\dfrac{1}{2}+\dfrac{\sqrt{5}}{2}i$
- $latex m=-2$
- $latex m=1$
- $latex m=-1$
- $latex m=0$
Hướng dẫn giải
Chuyển máy tính về phương thức COMPLEX w2
Thay $latex z=\dfrac{1}{2}+\dfrac{\sqrt{5}}{2}i$ vào phương trình $latex 2{{z}^{2}}+\left( m-1 \right)z+3=0$ ta được $latex 2{{\left( \dfrac{1}{2}+\dfrac{\sqrt{5}}{2}i \right)}^{2}}+\left( m-1 \right)\left( \dfrac{1}{2}+\dfrac{\sqrt{5}}{2}i \right)+3=0$
Suy ra: $latex m=\dfrac{-3-2{{\left( \dfrac{1}{2}+\dfrac{\sqrt{5}}{2}i \right)}^{2}}}{\dfrac{1}{2}+\dfrac{\sqrt{5}}{2}i}+1=-1$
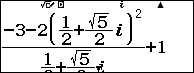
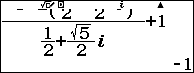
Đáp án C
Bài toán 2: Cho số phức $latex z=2+3i$ và $latex w=x+yi$ là một trong hai căn bậc hai của $latex z$. Tính $latex {{x}^{4}}+{{y}^{4}}$
- $latex \dfrac{17}{2}$
- $latex \dfrac{17}{4}$
- $latex 8$
- $latex 9$
Hướng dẫn giải
Sử dụng máy tính Casio fx 580 vnx tìm căn bậc hai của $latex z=2+3i$ và lưu vào A
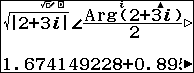
Tìm và lưu phần thực, phần ảo của $latex \sqrt{z}$ vào các ô nhớ B, C
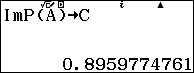
Vậy ta tìm được $latex {{x}^{4}}+{{y}^{4}}$
Mở rộng:
Bên cạnh việc sử dụng các tính năng của máy tính Casio fx 580vnx chúng ta có thể sử dụng tính chất của số phức để giải nhanh bài toán trên
Ta có $latex w=x+yi$ là căn bậc hai của $latex z=2+3i$. Suy ra $latex \left\{ \begin{align} & {{x}^{2}}-{{y}^{2}}=2 \\ & 2xy=3 \\\end{align} \right.$
Vậy: $latex {{x}^{4}}+{{y}^{4}}={{\left( {{x}^{2}}-{{y}^{2}} \right)}^{2}}+2{{x}^{2}}{{y}^{2}}={{2}^{2}}+2{{\left( \dfrac{3}{2} \right)}^{2}}=\dfrac{17}{2}$
Bài toán 3: Gọi $latex {{z}_{1}},{{z}_{2}},{{z}_{3}},{{z}_{4}}$ là 4 nghiệm của phương trình. Tính giá trị $latex T=\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|+\left| {{z}_{3}} \right|+\left| {{z}_{4}} \right|$
- $latex 2+2\sqrt{3}$
- $latex 2-2\sqrt{3}$
- $latex 2+\sqrt{3}$
- $latex 2-\sqrt{3}$
Bình luận:
[dropshadowbox align=”none” effect=”lifted-both” width=”auto” height=”” background_color=”#ffffff” border_width=”1″ border_color=”#dddddd” ]So với các dòng Casio 570VN plus, máy tính Casio fx 580 vnx đã nâng cấp bổ sung thêm tính năng giải phương trình bậc 4 và lưu nghiệm tìm được vào các ô nhớ của máy. Điều này giúp chúng ta thuận lợi hơn rất nhiều khi giải quyết các bài toán liên quan đến phương trình bậc 4 nghiệm phức[/dropshadowbox]Hướng dẫn giải
Sử dụng Casio fx 580 vnx để giải và lưu các nghiệm của phương trình bậc 4 vào ô nhớ A, B, C và D: $latex {{x}^{4}}-3{{x}^{3}}+6{{x}^{2}}-5x+3=0$
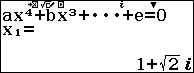
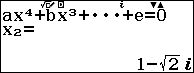
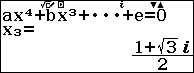
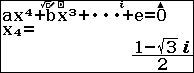
Như vậy ta có $latex T=\left| {{z}_{1}} \right|+\left| {{z}_{2}} \right|+\left| {{z}_{3}} \right|+\left| {{z}_{4}} \right|=\left| A \right|+\left| B \right|+\left| C \right|+\left| D \right|$
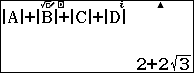
Đáp án A
Bài toán 4: Giải phương trình $latex {{z}^{2}}-8\left( 1-i \right)z+63-16i=0$
Hướng dẫn giải:
Lưu các giá trị $latex a=1;b=-8+8i;c=63-16i$ vào các ô nhớ
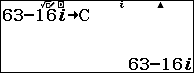
Tính$latex \Delta $:
$latex \Delta ={{b}^{2}}-4ac=-252-64i$ $latex \Rightarrow \sqrt{\Delta }=2-16i$
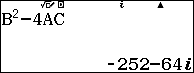
Vậy phương trình trên có 2 nghiệm
Bài toán 5: Tìm số phức $latex A$ để phương trình $latex {{z}^{2}}+Az+3i=0$ có tổng bình phương hai nghiệm bằng $latex 8$
Hướng dẫn giải:
Áp đụng định lý Vi-et vào phương trình $latex {{z}^{2}}+Az+3i=0$ ta có: $latex {{z}_{1}}+{{z}_{2}}=-A$ và $ {{z}_{1}}{{z}_{2}}=3i\\$
$latex z_{1}^{2}+z_{2}^{2}=8$
$latex \Leftrightarrow {{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}-2{{z}_{1}}{{z}_{2}}=8$
$latex \Leftrightarrow {{A}^{2}}-6i=8$ $latex \Leftrightarrow A=\sqrt{8+6i}$
Để tìm căn bậc 2 của số phức $latex 8+6i$ trên máy tính Casio fx 580 vnx ta có 2 cách sau:
Cách 1: Các phép toán trong phương thức COMPLEX w2
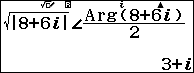
Vậy $latex A=\sqrt{8+6i}=\pm \left( 3+i \right)$
Cách 2: Sử dụng tính năng của các phím bấm Pol và Rec trên w1
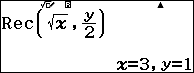
Như vậy ta có $latex A=3+i$ và $latex A=-3-i$
Cảm ơn các bạn đã theo dõi bài viết SỬ DỤNG CASIO FX 580VNX GIẢI QUYẾT CÁC BÀI TOÁN CĂN BẬC HAI CỦA SỐ PHỨC VÀ PHƯƠNG TRÌNH NGHIỆM PHỨC . Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO.
About Ngọc Hiền Bitex
