BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
Ứng dụng tích phân tính thể tích khối tròn xoay
- 13/12/2018
- 50,793 lượt xem
Thể tích khối tròn xoay là một phần của ứng dụng tích phân thường xuất hiện trong các đề thi toán lớp 12 cũng như kỳ thi Quốc gia. Trong bài viết này, chúng tôi sẽ hướng dẫn cách sử dụng máy tính CASIO fx 580VNX để có thể tính nhanh, chính xác thể tích khối tròn xoay thông qua một vài ví dụ
Bài toán 1:Cho hình $latex (H)$ giới hạn bởi đồ thị của các hàm số $latex y=f(x)$, $latex y=g(x)$ , $latex x=a;x=b$ quay quanh trục Ox tạo thành vật thể khối tròn xoay có thể tích bằng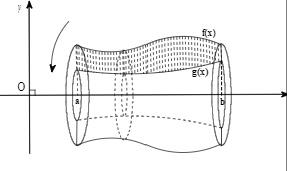
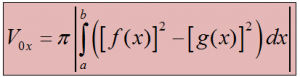
Bài toán 2: Cho hình $latex (H)$ giới hạn bởi đồ thị của các hàm số $latex x=f(y)$, $latex x=g(y)$ , $latex y=a;y=b$ quay quanh trục Oy tạo thành vật thể khối tròn xoay có thể tích bằng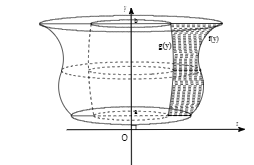 
Chú ý:
Nếu đề bài không có cho hai giả thiết $latex x=a;x=b$(hay $latex y=a;y=b$ ) thì trước khi áp dụng công thức $latex {{V}_{0x}}$(${{V}_{0y}}$ ) ta phải tìm hai cận của tích phân bằng cách giải phương trình giao điểm $latex f(x)=g(x)$ (hoặc $latex f(y)=g(y)$ )
Mở rộng: Cho hình $(H)$ giới hạn bởi đồ thị của các hàm số $latex y=f(x)$, $latex y=g(x)$ , $latex y=h(x)$ quay quanh trục Ox tạo thành vật thể khối tròn xoay
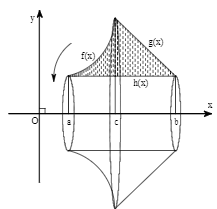Bước 1: Tìm các giao điểm a, b,c là nghiệm của các phương trình $f(x)=h(x);f(x)=g(x)$ và $g(x)=h(x)$
Bước 2: Áp dụng công thức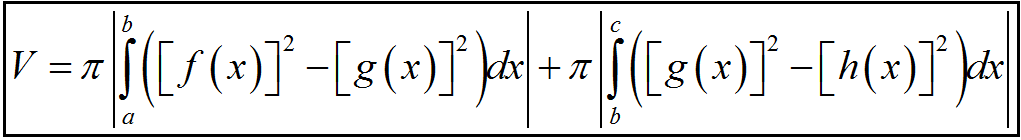
Ví dụ 1: Tính thể tích khối tròn xoay được tạo thành khi quay hình (H) giới hạn bởi đồ thị hàm số $latex y=\sqrt{s\text{inx}}$ , trục hoành, $latex x=0$ và $latex x=\frac{\pi }{2}$ quanh trục Ox.
A. $latex 1$ B. $latex \frac{\pi }{2}$ C. $latex 2\pi $ D. $latex \pi $
Hướng dẫn giải:
Công thức tính thể tích $latex V=\pi \int\limits_{0}^{\frac{\pi }{2}}{{{(\sqrt{\operatorname{s}\text{inx}})}^{2}}dx}$
Sử dụng máy tính Casio fx580vnx để tính tích phân trên
qKy(sjQ()$)dR0EqKa2=
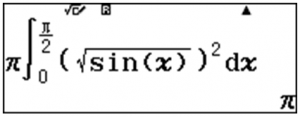
Đáp án: D
Chú ý: Trước khi thực hiện phép tính ta cần chuyển máy tính về chế độ Radian (xem hướng dẫn tại đây)
Ví dụ 2: Cho miền D giới hạn bởi hai đồ thị $latex y=4-{{x}^{2}}$ và $y={{x}^{2}}+2$. Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox.
A. $latex 16\pi $ B. $latex \frac{8}{3}\pi $ C. $latex 12\pi $ D. $latex \pi$
Hướng dẫn giải:
Nhận xét: Vì đề bài không cho hai cận của tích phân do đó đầu tiên chúng ta phải tìm hoành độ giao điểm của hai hàm số đã cho
Dùng máy tính Casio fx 580vnx để tìm nghiệm của phương trình: $latex 4-{{x}^{2}}={{x}^{2}}+2$
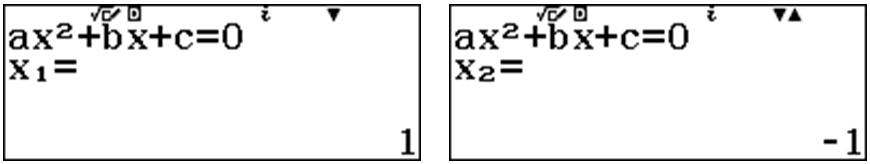
Công thức: $latex V=\pi \left| \int\limits_{-1}^{1}{\left[ {{(4-{{x}^{2}})}^{2}}-{{({{x}^{2}}+2)}^{2}} \right]}dx \right|$
Sử dụng máy tính Casio fx 580vnx để tính tích phân trên
qKq(y(4p[d)dp([d+2)dRp1E1=
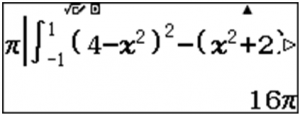
Ví dụ 3: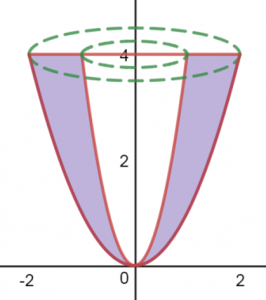 
Cho miền D giới hạn bởi hai đồ thị $latex y={{x}^{2}}$; $latex y=4{{x}^{2}}$ và $latex y=4$. Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Oy (như hình)
A. $latex 12\pi $ B. $latex 2\pi $ C. $latex 6\pi $ D. $latex 8\pi $
Hướng dẫn giải:
Chuyển đổi hàm số:
$latex y={{x}^{2}}\Rightarrow x=\sqrt{y}$ và $latex y=4{{x}^{2}}\Rightarrow x=\frac{\sqrt{y}}{2}$
Nhận xét: ta có đồ thị $latex y={{x}^{2}}$ và $latex y=4{{x}^{2}}$ giao nhau tại O. Do đó ta có $latex V=\pi \left| \int\limits_{0}^{4}{\left( {{(\sqrt{y})}^{2}}-{{\left( \frac{\sqrt{y}}{2} \right)}^{2}} \right)}dy \right|$
Sử dụng máy tính Casio fx 580vnx để tính tích phân trên
qKy[pa[R4R0E4=
Đáp án: C
Nhận xét: Đối với một số biểu thức đơn giản ta có thể khai triển để việc bấm máy trở nên nhanh và dễ dàng hơn
Ví dụ 4: Cho miền D giới hạn bởi đồ thị $latex (C):y={{x}^{2}}+1(x\ge 0)$và hai đường thẳng $latex y=-3x+11$ ;$latex y=2$. Tính thể tích khối tròn xoay được tạo nên do D quay quanh trục Ox
Hướng dẫn giải:
Tìm giao điểm của các đồ thị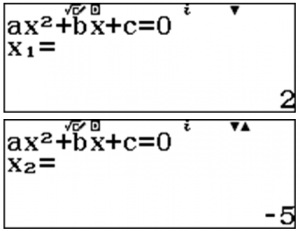
- $latex {{x}^{2}}+1=2\Rightarrow x=1$ (vì $x>0$ )
- $latex -3x+11=2\Rightarrow x=3$
- $latex {{x}^{2}}+1=-3x+11\Rightarrow x=2$ (vì $x=-5<0$ )
Công thức tính thể tích khối tròn xoay: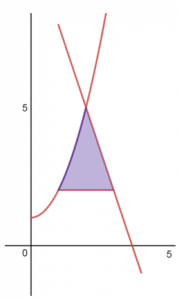
$latex V=\pi \int\limits_{1}^{2}{\text{ }\!\![\!\!\text{ }{{({{x}^{2}}+1)}^{2}}-4\text{ }\!\!]\!\!\text{ }dx}+\int\limits_{2}^{3}{\text{ }\!\![\!\!\text{ }{{(-3x+11)}^{2}}-4]dx}$
Sử dụng máy tính Casio fx 580vnx để tính tích phân trên
– Hết –
About Ngọc Hiền Bitex
