BITEXEDU Chuyên trang chia sẻ tài liệu, kinh nghiệm ứng dụng giải toán trên máy tính cầm tay
BIẾN ĐỔI CÔNG THỨC HỆ THỨC LƯỢNG ĐỂ CHỨNG MINH TAM GIÁC CÂN
- 18/12/2018
- 1,183 lượt xem
Hệ thức lượng trong tam giác là nội dung quan trọng trong chương trình Trung học phổ thông. Tiếp nối bài viết Một số bài toán cơ bản về hệ thức lượng trong tam giác và Biến đổi công thức hệ thức lượng để chứng minh tam giác vuông bài viết này sẽ giới thiệu về bài toán chứng minh tam giác vuông bằng phương pháp biến đổi hệ thức lượng
Bài toán : Cho $latex G$ là trọng tâm của $latex \Delta ABC$. Chứng minh rằng nếu $latex AB+GC=AC+GB$ thì $latex \Delta ABC$ là tam giác cân.
Nhận xét: Quan sát giả thiết bài toán ta thấy vai trò của $latex B$ và $latex C$ như nhau nên ta dự đoán $latex \Delta ABC$ cân tại $latex A$. Do đó ta cần chứng minh $latex AB=AC$
Hướng dẫn giải:
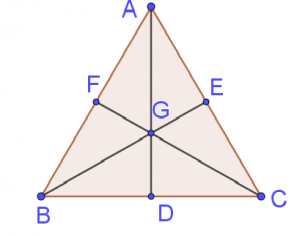
Do $latex G$ là trọng tâm của $latex \Delta ABC$ nên ta có:
$latex GA=\dfrac{2}{3}AD$ ; $latex GB=\dfrac{2}{3}BE$; $latex GC=\dfrac{2}{3}CF$
Áp dụng định lý đường trung tuyến trong $latex \Delta ABC$ ta có:
$latex BE=\dfrac{\sqrt{2\left( A{{B}^{2}}+B{{C}^{2}} \right)-A{{C}^{2}}}}{2}\Rightarrow GB=\dfrac{\sqrt{2\left( A{{B}^{2}}+B{{C}^{2}} \right)-A{{C}^{2}}}}{3}$
Tương tự ta có:
$latex GC=\dfrac{\sqrt{2\left( A{{C}^{2}}+B{{C}^{2}} \right)-A{{B}^{2}}}}{3}$
Ta có:
$latex AB+GC=AC+GB$
$latex \begin{align} & \Leftrightarrow AB+\dfrac{\sqrt{2\left( A{{C}^{2}}+B{{C}^{2}} \right)-A{{B}^{2}}}}{3}=AC+\dfrac{\sqrt{2\left( A{{B}^{2}}+B{{C}^{2}} \right)-A{{C}^{2}}}}{3} \\ & \Leftrightarrow \sqrt{2\left( A{{C}^{2}}+B{{C}^{2}} \right)-A{{B}^{2}}}-\sqrt{2\left( A{{B}^{2}}+B{{C}^{2}} \right)-A{{C}^{2}}}=3\left( AC-AB \right) \\ & \Leftrightarrow \dfrac{A{{C}^{2}}-A{{B}^{2}}}{\sqrt{2A{{C}^{2}}+2B{{C}^{2}}-A{{B}^{2}}}+\sqrt{2A{{B}^{2}}+2B{{C}^{2}}-A{{C}^{2}}}}=AC-AB \\\end{align}$
Giả sử: $latex AB<AC$
Do $latex BC>AC-AB$ nên ta có
$latex \sqrt{2A{{C}^{2}}+2B{{C}^{2}}-A{{B}^{2}}}+\sqrt{2A{{B}^{2}}+2B{{C}^{2}}-A{{C}^{2}}}$
$latex \begin{align} & >\sqrt{2A{{C}^{2}}+2{{\left( AC-AB \right)}^{2}}-A{{B}^{2}}}+\sqrt{2A{{B}^{2}}+2{{\left( AC-AB \right)}^{2}}-A{{C}^{2}}} \\ & =\sqrt{4A{{C}^{2}}+A{{B}^{2}}-4AB.AC}+\sqrt{4A{{B}^{2}}+A{{C}^{2}}-4AB.AC} \\ & =\sqrt{{{\left( 2AC-AB \right)}^{2}}}+\sqrt{{{\left( 2AB-AC \right)}^{2}}} \\ & =2AC-AB+\left| 2AB-AC \right| \\\end{align}$
Suy ra:
$latex \dfrac{AC+AB}{\left| 2AB-AC \right|+2AC-AB}>1$ (1)
Giả sử $latex AC<2AB$ thì
$latex \left( 1 \right)\Leftrightarrow \dfrac{AC+AB}{2AB-AC+2AC-AB}>1$
$latex \left( 1 \right)\Leftrightarrow 1>1$ (vô lý)
Giả sử $latex AC\ge 2AB$thì
$latex \left( 1 \right)\Leftrightarrow \dfrac{AC+AB}{AC-2AB+2AC-AB}>1$
$latex \left( 1 \right)\Leftrightarrow AC+AB>AC-3AB$
$latex \left( 1 \right)\Leftrightarrow 2AB>AC$ (Vô lý)
Như vậy $latex AB<AC$ là không thể xảy ra
Tương tự không thể xảy ra trường hợp $latex AC<AB$
Suy ra $latex AB=AC$.
Vậy $latex \Delta ABC$ cân tại$latex A$
Cảm ơn các bạn đã theo dõi bài viết BIẾN ĐỔI CÔNG THỨC HỆ THỨC LƯỢNG ĐỂ CHỨNG MINH TAM GIÁC CÂN. Mọi ý kiến đóng góp và các câu hỏi thắc mắc về bài viết cũng như các vấn đề về máy tính Casio fx 580vnx , bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO.
About Ngọc Hiền Bitex
